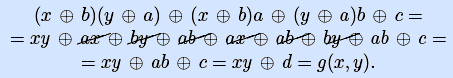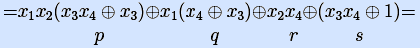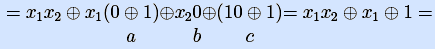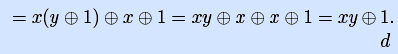не умаляя общности что значит

Рецензии на произведение «Вариации на тему Гёделя, или Тезисы Мата»

И снова математика.

Ещё в институте, на лекциях по Дискретной Математике( графы, Машина Тьюринга, Теория Чисел), мне «не нравились» аксиомы, вошедшие в эту дисциплину с лёгкой руки Джузеппе Пиано.

Так вот, одна из этих аксиом гласит:

На мой взгляд, теорема Гёделя о неполноте как раз и доказала правильность такого подхода к так называемым натуральным числам.

Лучше скажите — является ли математика инструментом познания окружающего мира, или она всего лишь заложница законов человеческой психики?

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.

© Все права принадлежат авторам, 2000-2021. Портал работает под эгидой Российского союза писателей. 18+

Источник

Не умаляя общности что значит

Рассмотрим следующее разложение булевой функции f(x₁, …, x_n) по переменной x_i.

Разложение Шеннона. f(x₁, …, x_n) = x_i f(x₁, …, x_i-1,1,x_i+1, …, x_n) x _i f(x₁, …, x_i-1,0,x_i+1, …, x_n).

Доказательство (не умаляя общности, для i=1). При x₁=0 имеем:

f(0,x₂, …, x_n)=0f(1,x₂, …, x_n) 0 f(0,x₂, …, x_n)=f(0,x₂, …, x_n).

f(1,x₂, …, x_n)=1f(1,x₂, …, x_n) 1 f(0,x₂, …, x_n)=f(1,x₂, …, x_n).

Следовательно, разложение верно. •

Определение. Сомножитель f(x₁, …, x_i-1,1,x_i+1, …, x_n) называется коэффициентом разложения функции f(x₁, …, x_n) по переменной x_i при x_i, а сомножитель f(x₁, …, x_i-1,0,x_i+1, …, x_n) – коэффициентом разложения функции f(x₁, …, x_n) по переменной x_i при x _i.

Пример. Булеву функцию f(x,y,z)= y x z yz разложим по переменной x:

[ упростим коэффициенты разложения на основе свойств 0 и 1 для конъюнкции ]

[ продолжим упрощение коэффициента при x на основе свойства 0 для эквивалентности a 0 = a при a= y ; напомним, что способ получения таких свойств был рассмотрен в подразделе 4.4 ]

в результате имеем следующие коффициенты разложения, зависящие лишь от y и z:

y z yz – коэффициент разложения функции f(x,y,z) по переменной x при x,

Источник

Не умаляя общности что значит

Пусть a, b, c – положительные числа, сумма которых равна 1. Докажите неравенство:

Решение 1

Заметим, что (мы использовали неравенство между средним арифметическим и средним гармоническим для положительных x, y). Осталось сложить три аналогичных неравенства.

Решение 2

Не умаляя общности, можно считать, что a ≥ b ≥ c, тогда 1 – c² ≥ 1 – b² ≥ 1 – a² и, следовательно,

Заметим, что Таким образом, нужно доказать неравенство
Поскольку сумма числителей равна 0, неравенство будет доказано, если мы заменим знаменатели на равные таким образом, что каждая дробь при этом не увеличится. Если a ≥ b ≥ ⅓ ≥ c, то заменим все знаменатели на 1 – c², в результате отрицательное слагаемое не изменится, а положительные не увеличатся. Если a ≥ ⅓ b ≥ c, то заменим все знаменатели на 1 – b², тогда положительное слагаемое и одно из отрицательных только уменьшатся, а второе отрицательное слагаемое останется неизменным.

Источники и прецеденты использования

Источник

СНМ с операцией удаления за О(1)

Содержание

Описание [ править ]

Структура данных должна поддерживать следующие операции:

В дальнейшем используются следующие понятия и обозначения:

Идея [ править ]

В реализации СНМ с помощью леса корневых деревьев нет возможности удалить произвольную вершину из множества за разумное время — в таком случае придется переподвешивать [math]O(n) [/math] поддеревьев этой вершины. Однако, если вершина является листом, то ее можно удалять совершенно безболезненно.

Все дальнейшие усилия направлены на то, чтобы поддержать эти [math]2[/math] операции, не испортив при этом асимптотику всех остальных.

Реализация [ править ]

Расширение структуры данных [ править ]

Расширим лес корневых деревьев следующим образом:

Модификации для 1-го соображения [ править ]

Разделим понятия вершина дерева и элемент множества:

Модификации для 2-го соображения [ править ]

Эти три нововведения необходимы для нахождения листа в дереве (как оказывается, это гораздо более нетривиальная задача).

Введем также следующие определения:

В нашей структуре данных будет поддерживаться следующий инвариант: дерево всегда полное или сокращенное. Этот инвариант влечет за собой очевидные следствия:

Реализация операции Makeset [ править ]

Реализация операции Union [ править ]

Если в качестве идентификаторов множеств нам переданы произвольные представители этих множеств, нам придется запустить процедуру [math]\mathrm [/math] для каждого из них, чтобы найти корни деревьев. Без учета вызова процедуры [math]\mathrm [/math] мы сделаем [math]O(1)[/math] операций.

Реализация операции Find [ править ]

Операция Relink [ править ]

Реализуем процедуру [math] \mathrm < Relink(x) >[/math] — переподвешивание элемента [math]x[/math] к его «дедушке» с сохранением инвариантов и структуры списков.

Очевидно, что [math]\mathrm [/math] выполняется за [math]O(1)[/math]

Операция Find [ править ]

Реализуем собственно операцию [math]\mathrm[/math] :

Реализация операции Delete [ править ]

Операция ReducedTreeDelete [ править ]

Операция FindLeaf [ править ]

Операция DeleteLeaf [ править ]

Пусть [math]x[/math] — удаляемый лист.

Следующие [math]2[/math] шага обеспечивают сохранение полноты дерева

Итак, соберем воедино операцию [math]\mathrm[/math] :

Операция Delete [ править ]

Пусть элемент [math]a[/math] ассоциирован с вершиной [math]x[/math]

Анализ [ править ]

Основные положения [ править ]

Инвариант 3 [math]VAL(A) \geqslant 2^ [/math]

[math] 2^ \leqslant VAL(A) \leqslant |A| \left(\frac<3> <2>\right)^ \newline \newline |A| \geqslant \frac <2^> <\left(\frac<3> <2>\right)^> = \left( \frac <4> <3>\right)^ \newline \newline rank(A) \leqslant \log_< \frac<4> <3>> < (|A|) >= O(\log <|A|>) = O(\log) [/math]

Докажем теперь, что каждая из операций сохраняет инвариант 3.

Makeset [ править ]

Т. к. операция [math]\mathrm[/math] создает сокращенное дерево, то по лемме 1 [math]\mathrm[/math] сохраняет инвариант 3

Union [ править ]

Пусть для множеств [math]A[/math] и [math]B[/math] инвариант 3 выполняется.

[math]VAL(C) \gt VAL(A) \geqslant 2^ = 2^[/math]

Следовательно, операция [math]\mathrm[/math] сохраняет инвариант 3.

Find [ править ]

Пусть для множества [math]A[/math] инвариант 3 выполняется.

Осталось рассмотреть другой случай — когда до и после выполнения [math]\mathrm \; T_A[/math] было полным. Обозначим множество [math]A[/math] после выполнения [math]\mathrm[/math] как [math]A'[/math]

Анализ операции Relink [ править ]

[math]VAL(A’) \geqslant VAL(A) \geqslant 2^ = 2^[/math]

Итак, операция [math]\mathrm[/math] сохраняет инвариант 3, следовательно — операция [math]\mathrm[/math] сохраняет инвариант 3.

Delete [ править ]

Пусть для множества [math]A[/math] инвариант 3 выполняется.

Если после выполнения [math]\mathrm \; T_A[/math] стало сокращенным, то инвариант 3 сохранен по лемме 1.

Осталось рассмотреть случай, когда до и после выполнения [math]\mathrm \; T_A[/math] было полным. Обозначим множество [math]A[/math] после выполнения [math]\mathrm[/math] как [math]A'[/math]

Анализ операции DeleteLeaf [ править ]

[math]VAL(A’) \geqslant VAL(A)[/math]

[math]\mathrm [/math] меняет [math] rank(A) [/math] только когда дерево становится сокращенным, а мы рассматриваем только полные, следовательно — [math] rank(A) [/math] не меняется, следовательно:

[math]VAL(A’) \geqslant VAL(A) \geqslant 2^ = 2^[/math]

[math]VAL(A’) \geqslant VAL(A) \geqslant 2^ = 2^[/math]

Итак, операция [math]\mathrm[/math] сохраняет инвариант 3, а значит, и операция [math]\mathrm [/math] сохраняет его.

Источник

Не умаляя общности что значит

Определение. Булева функция называется линейной (принадлежит классу L), если ее полином Жегалкина линеен.

Примеры. Мажоритарная функция не является линейной: степень ее полинома Жегалкина (xy xz yz) равна 2. Из элементарных булевых функций линейными являются, например, инверсия и эквивалентность. Не являются линейными, например, штрих Шеффера и стрелка Пирса. •

Доказательство. Полином Жегалкина линейной функции f(x₁, …, x_n) имеет вид:

Пример. Из всех 16 булевых функций двух аргументов x₁, x₂ 8 функций (2 2+1 ) принадлежат классу L: 0, 1, , , тождественные функции x₁ и x₂ и их инверсии x ₁ и x ₂. •

Теорема о замкнутости класса L. Множество всех линейных булевых функций является замкнутым классом.

Доказательство. Рассмотрим суперпозицию любых булевых функций из L, то есть функцию

и покажем, что она является линейной. Представим каждую из функций, образующих суперпозицию, полиномом Жегалкина:

Подставив эти полиномы в суперпозицию, получим:

Поскольку в последней формуле каждая скобка есть булева константа, то получен линейный полином Жегалкина. Значит, функция f(x₁, …, x_n) линейная, и класс L замкнут. •

В первых трех группах вынесем за скобки соответственно x₁x₂, x₁ и x₂ :

где a, b, c – булевы константы.

Если a=b=c=0, конъюнкция получена. Иначе положим в последней формуле x₁= x b, и x₂ = y a (подстановка переменных x, y и их инверсий x 1, y 1 допустима по условию теоремы), раскроем скобки и удалим пары одинаковых конъюнкций:

Если булева константа d=0, конъюнкция xy получена. Иначе функция g(x,y)= x y. Тогда, инвертировав исходную функцию (что допустимо по условию теоремы), получим конъюнкцию xy. •

Пример. Рассмотрим нелинейную булеву функцию, заданную полиномом Жегалкина.

[ выберем первую конъюнкцию x₁x₂ x₃x₄, в ней выберем переменные x₁, x₂ и сгруппируем конъюнкции ]

[ p(x₃,x₄)=1 при x₃=1, x₄=0, подставим эти значения переменных в формулу ]

[ положим x₁=x b = x, x₂ =y a=y 1 ]

Инвертировав исходную функцию, получим конъюнкцию xy. •

Источник

• ← морщинистые руки что делать чем лечить
• что случилось в раменском районе сегодня →