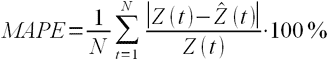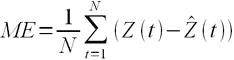что такое bias в прогнозировании

Точность прогнозирования

Любому человеку, который занимается прогнозированием продаж, важно и необходимо оценивать корректность своих прогнозов. Для этого существует такой показатель, как «Точность прогнозирования». В данной статье именно о нем я и расскажу.

Хочу обратить внимание на то, что в некоторых компаниях данный показатель называют «Аккуратность прогнозирования». Не могу сказать, что это неправильно, но в данной статье будет фигурировать именно «Точность прогнозирования». Ведь мы оцениваем насколько точно наш прогноз совпадает с фактическими значениями, а не аккуратность, с которой мы его высчитывали.

Точность прогнозирования — это показатель, который характеризует качество прогноза. Он отражает насколько сформированный прогноз совпадает с истинными фактическими значениями.

«Точность прогнозирования»: формула, разновидности «ошибок прогноза».

Итак, чтобы рассчитать точность прогнозирования, необходимо сначала рассчитать ошибку прогнозирования в процентах, а затем, вычесть ее из 100%:

В качестве основной ошибки для расчета точности прогнозирования мы будем использовать Взвешенную Абсолютную Процентную Ошибку (WAPE — Weighted Absolute Percent Error), которая рассчитывается по формуле:

То есть: сумма всех отклонений прогноза от факта по модулю, деленное на сумму всех фактов и умноженное на 100%.

Важно! Если ошибка прогнозирования больше 100%, то точность прогнозирования всегда будет равна 0%.

Вообще, помимо WAPE (которую также называют MAD-Mean Ratio), существует множество ошибок, которые мы можем использовать в качестве основной ошибки для расчета точности прогнозирования. Например:

И так далее (более подробно смотрите здесь). Однако при расчете точности прогнозирования, WAPE — наиболее оптимальный вариант ошибки, так как он наименее чувствителен к выбросам и искажениям, а также интуитивно-понятен и прост в расчете. В общем, WAPE — наш выбор!

Итоговая формула примет вид:

Про другие ошибки здесь я писать не буду, потому что и использовать мы их не будем, но если у Вас есть желание ознакомиться с ними, рекомендую к прочтению статьи «A survey of forecast error measures» и «Another look at measures of forecast accuracy», а также книгу «Forecasting: Principles and Practice». К сожалению, русскоязычной информации на просторах всемирной сети на эту тематику не очень много, поэтому для изучения материала необходимы минимальные знания английского языка.

Примеры расчета точности прогнозирования:

Итак, формула расчета точности у нас есть, теперь мы перейдем непосредственно к примеру расчета:

Все просто. У нас есть исходные данные: SKU, факт продаж и прогноз продаж. Для каждого SKU мы находим отклонения по модулю (|факт-прогноз|), а затем суммируем их, получаем 126. Затем суммируем все фактические показатели, получаем 468. Находим ошибку прогнозирования: делим сумму отклонений на сумму фактических показателей — 126/468 = 0,269, то есть 27%. И вычитаем значение ошибки прогнозирования из 100% и получаем точность 73%. Средний результат.

Также, бывают ситуации, когда необходимо рассчитать не общую точность по всем номенклатурам, а отдельно по каждому клиенту (или номенклатурной группе, или по каналам продаж и т.д.). На таблице ниже изображен изображен именно такой пример:

Суть расчетов не меняется, только теперь находим сумму отклонений и сумму фактов для каждого из клиентов по отдельности. Для первого клиента ошибка прогнозирования равна 126/468 = 27%, соответственно точность равна 73% (то же самое, что и в первом примере), а для второго клиента ошибка прогнозирования равна 206/662 = 31%, и точность равна 69%.

В общем-то и все. Мы нашли точность прогнозирования отдельно для списка SKU и отдельно по каждому клиенту. Важно(!) помнить некоторые правила:

Файл с примерами из статьи можно скачать здесь.

Источник

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Источник

Анализ малых данных

КвазиНаучный блог Александра Дьяконова

Смещение (bias) и разброс (variance)

Сегодня дадим немного объяснений стандартных для машинного обучения понятий: смещение, разброс, переобучение и недообучение. Как всегда, всё объясним просто (но нужна будет математическая подготовка), на картинках, с примерами (в данном случае на модельных задачах). Все рисунки и эксперименты авторские, в конце, по традиции, изюминка – в чём при объяснении этих понятий Вас обманывают на курсах по ML и в учебниках;)

Ниже обсудим несколько фундаментальных понятий машинного обучения. Первое – переобучение (overfitting) – явление, когда ошибка на тестовой выборке заметно больше ошибки на обучающей. Это главная проблема машинного обучения: если бы такого эффекта не было (ошибка на тесте примерно совпадала с ошибкой на обучении), то всё обучение сводилось бы к минимизации ошибки на тесте (т.н. эмпирическому риску).

Второе – недообучение (underfitting) – явление, когда ошибка на обучающей выборке достаточно большая, часто говорят «не удаётся настроиться на выборку». Такой странный термин объясняется тем, что недообучение при настройке алгоритмов итерационными методами (например, нейронных сетей методом обратного распространения) можно наблюдать, когда сделано слишком маленькое число итераций, т.е. «не успели обучиться».

Третье – сложность (complexity) модели алгоритмов (допускает множество формализаций) – оценивает, насколько разнообразно семейство алгоритмов в модели с точки зрения их функциональных свойств (например, способности настраиваться на выборки). Повышение сложности (т.е. использование более сложных моделей) решает проблему недообучения и вызывает переобучение.

Сначала опишем на примере, как проявляется проблема выбора сложности и почему возникает переобучение. Для начала рассмотрим задачу регрессии. Для простоты будем считать, что это регрессия от одного признака x. Целевая зависимость y(x) известна в конечном наборе точек. На рис. 1 показана выборка для зависимости вида y = sin(4x) + шум, на рис. 2 для зашумлённой пороговой зависимости.

Рис. 1. Настройка полиномов различных степеней на обучающую выборку. Рис. 2. Настройка полиномов различных степеней на обучающую выборку.

На рисунках показаны также решения указанных задач полиномиальной регрессией с разными степенями полиномов. Видно, что в обеих задачах полином первой степени явно плохо подходит для описания целевой зависимости, второй – достаточно хорошо её описывает, хотя ошибки есть и на обучающей выборке, седьмой – идеально проходит через точки обучающей выборки, но совсем не похож на «естественную функцию» и существенно отклоняется от целевой зависимости в остальных точках.

Если попробовать решить задачу полиномами различной степени, то мы получим рис. 3 (он построен для первой задачи, но во второй картина аналогичная). Видно, что с увеличением степени ошибка на обучающей выборке падает, а на тестовой (мы взяли очень мелкую сетку отрезка [0, 1]) – сначала падает, потом возрастает.

Рис. 3. Зависимость ошибки на обучении и тесте от степени полинома.

Попробуем разобраться, в чём дело с теоретической точки зрения (сейчас немного математики). Наша целевая зависимость имеет вид

Мы строим алгоритм (в нашем случае полином фиксированной степени) a=a(x), посмотрим чему равно математическое ожидание квадрата отклонения ответа алгоритма от истинного значения:

Здесь важно понимать, как берутся матожидания (т.е., по сути, интегрирования) в приведённых выше формулах. Мы считаем, что обучающая выборка выбирается случайно из некоторого распределения, настроенный алгоритм тоже случаен, поскольку зависит от выборки, настройка алгоритма также может быть стохастической. Таким образом, матожидание берётся по всем данным (обучающим выборкам) и настройкам алгоритма, а сами формулы записываются в конкретной точке x:

При желании, можно проинтегрировать полученные формулы и по всем объектам (точнее, по какому-то распределению всех объектов) и получить уже смещение и разброс модели алгоритмов как таковой.

Разбросом (variance) мы назвали дисперсию ответов алгоритмов Da, а смещением (bias) – матожидание разности между истинным ответом и выданным алгоритмом: E(f – a). Мы получили, что ошибка раскладывается на три составляющие. Первая связана с шумом в самих данных, а вот две остальные связаны с используемой моделью алгоритмов. Понятно, что разброс характеризует разнообразие алгоритмов (из-за случайности обучающей выборки, в том числе шума, и стохастической природы настройки), а смещение – способность модели алгоритмов настраиваться на целевую зависимость. Проиллюстрируем это. На рис. 4-5 – показаны различные полиномы первой степени, они настроены на разных обучающих выборках. В точке x=0.5 ответы алгоритмов являются случайными величинами, они немного «разбросаны» (есть variance), а также они сильно смещены (есть bias) относительно правильного ответа (который, кстати, даже если нам и известен, то с точностью до шума).

Рис. 4. Полиномы 1й степени, настроенные на разных обучающих выборках. Рис. 5. Шум, разброс и смещение при настройках полиномов 1й степени.

На рис. 6-7 изображены уже полиномы второй степени (настроенные на тех же выборках). В точке x=0.5 у них сильно меньше смещение и чуть меньше разброс. Видно, что они совсем неплохо описывают целевую зависимость во всех точках.

Рис. 6. Полиномы 2й степени, настроенные на разных обучающих выборках. Рис. 7. Шум, разброс и смещение при настройках полиномов 2й степени.

Рис. 8. Объяснение разброса и смещения на примере игры в дартс.

Ещё важный момент: спортсмен может повысить точность целясь выше/ниже/правее/левее, а для алгоритма нет таких понятий. Напомним, что разброс и смещение мы вводили в конкретной точке. Если изменить смещение в этой точке, то модель будет по-новому вести себя и в остальных. Если же усреднить смещение, точнее его квадрат, по всем точкам, то мы получим просто число (оно не указывает, как менять модель, чтобы уменьшить ошибку).

Теперь рассмотрим самую частую иллюстрацию, которую приводят при объяснении разброса и смещения, см. рис. 9. Она полностью согласуется с рис. 3. При увеличении сложности модели (например, степени полинома) ошибка на независимом контроле сначала падает, потом начинает увеличиваться. Обычно это связывают с уменьшением смещения (в сложных моделях очень много алгоритмов, поэтому наверняка найдутся те, которые хорошо описывают целевую зависимость) и увеличением разброса (в сложных моделях больше алгоритмов, а следовательно, и больше разброс).

Рис. 9. Классическая иллюстрация изменения разброса и смещения.

Для простых моделей характерно недообучение (они слишком простые, не могут описать целевую зависимость и имеют большое смещение), для сложных – переобучение (алгоритмов в модели слишком много, при настройке мы выбираем ту, которая хорошо описывает обучающую выборку, но из-за сильного разброса она может допускать большую ошибку на тесте).

Теперь рассмотрим задачу классификации. Отметим, что для неё тоже есть результат о разложении ошибки на шум, разброс и смещение. На рис. 10-12 показаны результаты экспериментов в задаче с двумя классами (стандартная задача «два полумесяца») и моделью k ближайших соседей (kNN) при разных k. Результат также согласуется с рис. 9, если учесть, что изображена точность, а не ошибка, и сложность алгоритма

1/k. Возникает вопрос, а почему так вводится сложность для kNN? Ведь при разных k эти алгоритмы

Всё очень просто: часто сложность как раз и логично формализовать как 1/variance. На рис. 11 показаны разделяющие поверхности метода 1NN для разных выборок, которые описывают одну и ту же целевую зависимость. Они очень сильно отличаются друг от друга. А разделяющие поверхности kNN при больших k, см. рис 12, различаются существенно меньше. И чем выше k, тем стабильней результат. В этом смысле это очень простые алгоритмы: то, как они разделяют классы, меньше зависит от исходных данных, т.е. по определению ответ алгоритма 9NN в каждой точке зависит от 9и ближайших соседей, а по факту он практически не меняется от выборки к выборке (при варьировании обучения).

Рис. 10. Точность метода kNN при разных k на обучении и контроле. Рис. 11. Разделяющие поверхности 1NN для разных выборок (одинаково распределённых). Рис. 12. Разделяющие поверхности 9NN для тех же выборок.

Теперь покажем, в чём не правы стандартные учебники и учебные курсы по машинному обучению. Проведём эксперименты по оцениванию разброса и смещения в модельных задачах. На рис. 13-14 приведены результаты для задачи с целевой зависимостью «ступенька», а на рис. 15-16 для задачи с целевой зависимостью «sin(4x)».

Рис. 13. «Средние» полиномы различных степеней в задаче «ступенька». Рис. 14. Ошибка при разных степенях полиномов в задаче «ступенька». Рис. 15. «Средние» полиномы различных степеней в задаче «синус». Рис. 16. Ошибка при разных степенях полиномов в задаче «синус».

Очевидно, что степень полинома – очень естественная мера сложности для полиномиальной регрессии. Но полученные рисунки немного отличаются от рис. 9:

Почему так происходит? Одна их причин в том, что «сложность модели», если мы хотим видеть красивые графики монотонных и унимодальных функций, правильнее определять для конкретных данных! Например, ступенчатая функция нечётная (с точностью до смещения) и для восстановления такой целевой зависимости лучше подходят полиномы с нечётной старшей степенью.

Кстати, если использовать полиномиальную регрессию с L2-регуляризацией, то на рис. 16 смещение начинает вести себя «по классике»: убывать при увеличении степени полинома.

П.С. Дальше возникают естественные вопросы: как найти оптимальную сложность модели, как решать задачу сложными моделями и не переобучаться (используют же нейросети). Но это тема для отдельного поста… Просьба к читателям – давать отклики в комментариях. Этот материал будет использован, в том числе, в рамках нового курса на ВМК МГУ, а также в книжке, которую автор уже и не надеется закончить… Поэтому любые замечания по формулировкам, корректности выводов и т.п. будут полезны. Удачи!

Источник

Что такое bias в прогнозировании

18 Янв Ошибка прогнозирования: как рассчитать и применять.

Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.

В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.

Статистические методы

Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.

В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.

MAPE – средняя абсолютная ошибка в процентах

где Z(t) – фактическое значение временного ряда, а – прогнозное.

Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

.

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N

8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

ME – средняя ошибка

Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).

MSE – среднеквадратичная ошибка

.

RMSE – квадратный корень из среднеквадратичной ошибки

.

SD – стандартное отклонение

где ME – есть средняя ошибка, определенная по формуле выше.

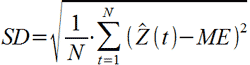
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Связь точности и ошибки прогнозирования

В начале этого обсуждения разберемся с определениями.

Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.

Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)

Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:

где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:

вариант

прогноз

факт

ошибка прогноза

Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:

В таком случае для тех же примеров ошибка рассчитается иначе:

вариант

прогноз

факт

ошибка прогноза

Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.

Визуальный метод – графический

Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.

По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.

Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.

Использование формул ошибки прогнозирования на практике

Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.

Пример расчета такой оценки Вы сможете увидеть в файле Excel.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.

Для чего используется ошибка прогнозирования

В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.

Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.

В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.

Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».

Источник