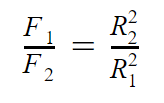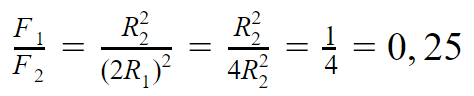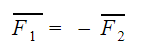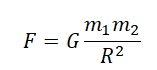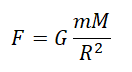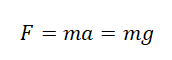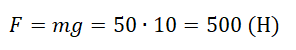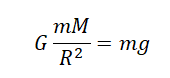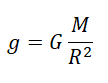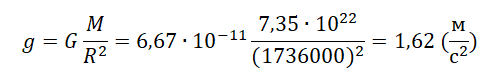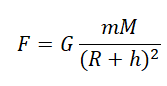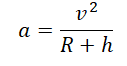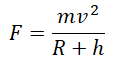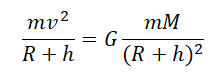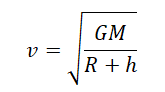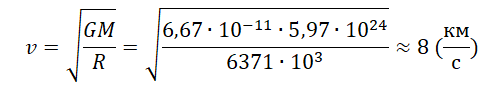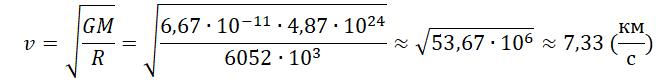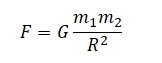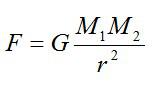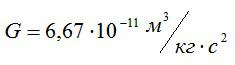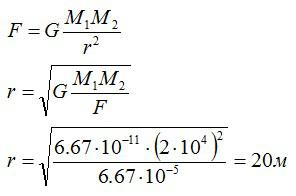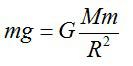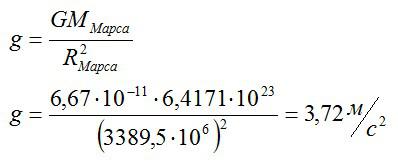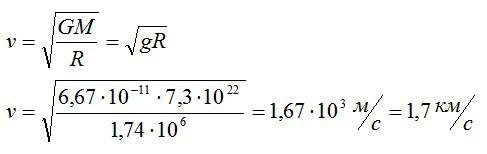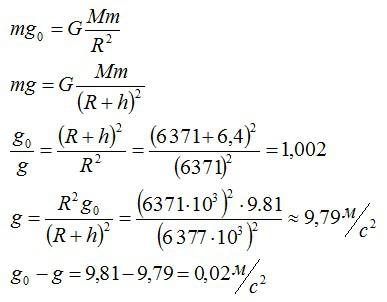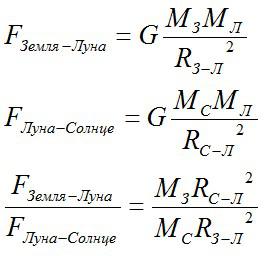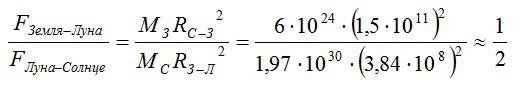Что нужно сделать чтобы увеличить силу тяготения

Закон всемирного тяготения

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

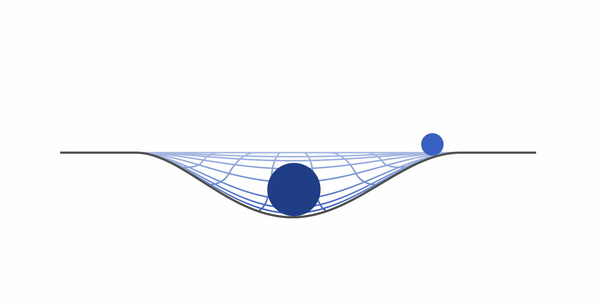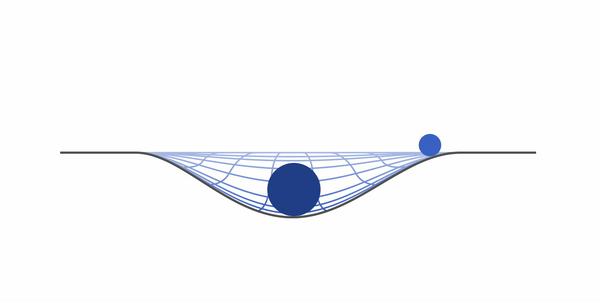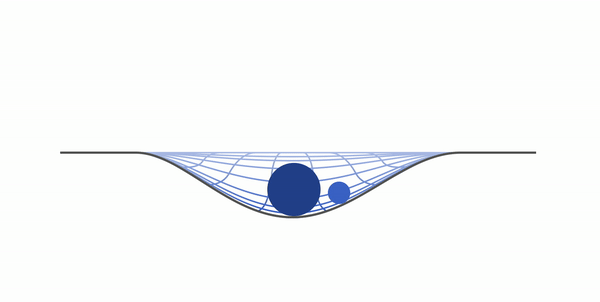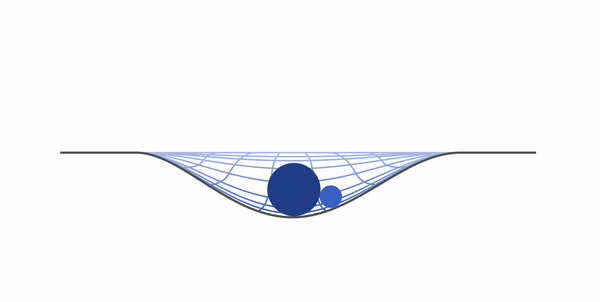
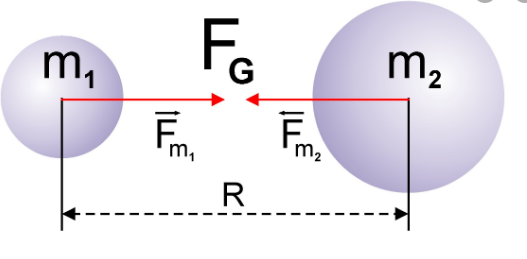
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

Закон всемирного тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁=2R₂.

Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести

F — сила тяжести [Н]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

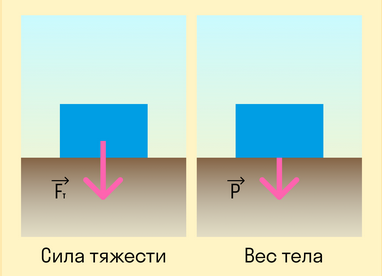
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

Приравниваем правые части:

Делим на массу левую и правую части:

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Закон всемирного тяготения

g — ускорение свободного падения [м/с 2 ]

M — масса планеты [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Но разве это не зависит еще и от массы предмета?

Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈

Третий закон Ньютона

F₁ — сила, с которой первое тело действует на второе [Н]

F₂ — сила, с которой второе тело действует на первое [Н]

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

Источник

Гравитационные силы. Закон всемирного тяготения.

теория по физике 🧲 динамика

Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.

Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.

Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.

F — сила всемирного тяготения, m₁и m₂ — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10 –11 Н ∙ м 2 /кг 2 ).

Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.

Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m₁= 1 кг и m₂= 1 кг, то F = G.

Сила тяжести

Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.

Сила тяжести — сила, с которой Земля притягивает к себе тела.

Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле

Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:

Вывод формулы ускорения свободного падения

Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.

Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.

Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:

Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:

Формула расчета ускорения свободного падения

Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.

Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10 22 кг.

Переведем километры в метры: 1736 км = 1736000 м.

Первая космическая скорость

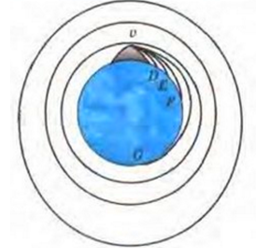
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

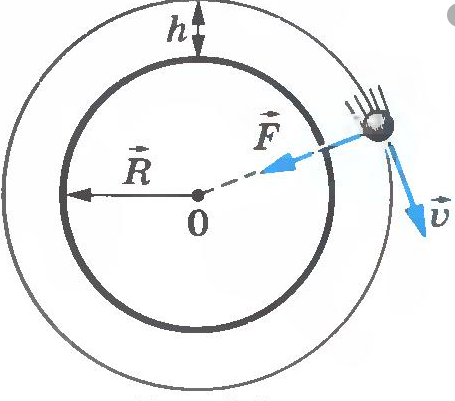
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.

Алгоритм решения

Решение

Запишем исходные данные:

Запишем закон всемирного тяготения:

Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m₁ и m₂.

R₂ больше R₁ втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

Источник

Задачи на закон всемирного тяготения с решением

Закон всемирного тяготения – фундаментальный закон природы, согласно которому все предметы притягиваются между собой. Это проявление гравитационного взаимодействия. Если хотите узнать о гравитации больше – читайте наш отдельный материал.

На своем телеграм-канале мы ежедневно отбираем полезную и интересную информацию. Подписывайтесь!

Закон всемирного тяготения: формулировка, примеры

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.

Примеры действия закона всемирного тяготения:

Вопросы на закон всемирного тяготения

Вопрос 1. Если все предметы притягиваются, то почему Луна не падает на Землю, Земля не падает на Солнце и т.д.?

Ответ. Все дело в скорости движения небесных тел. Луна движется вокруг Земли со скоростью равной примерно 1 км/с. Этой скорости недостаточно, чтобы покинуть орбиту, и достаточно, чтобы Луна не упала на Землю. Можно сказать, что Луна падает на Землю, но это падение никогда не заканчивается.

Вопрос 2. Что из этих величин является фундаментальной физической константой: гравитационная постоянная G или ускорение свободного падения g?

Ответ. Гравитационная постоянная G является одинаковой для всех тел в природе и в любой точке Вселенной. Ее значение:

Ускорение свободного падения g в пределах Земли варьируется в зависимости от координат и высоты подъема тела над поверхностью. На других планетах значение g будет совершенно иным, так как оно зависит от массы и размеров небесного тела.

Вопрос 3. Как развивалась теория тяготения после Ньютона и до наших дней?

Ответ. Классическая теория тяготения Ньютона господствовала в физике на протяжении более чем двух веков. В 1915 году Эйнштейн показал, что она является частным случаем общей теории относительности.

Вопрос 4. Что такое первая и вторая космические скорости?

Ответ. Первая космическая скорость – скорость, с которой спутник должен двигаться вокруг Земли или другого космического объекта, чтобы оставаться на орбите и не падать. Для Земли значение первой космической скорости равно 7,91 км/с.
Вторая космическая скорость – скорость, необходимая для того, чтобы покинуть орбиту небесного тела. Значение: 11,2 км/с.

Вопрос 5. С гравитационной постоянной разобрались. Ну а что такое гравитационная неустойчивость?

Ответ. Гравитационная неустойчивость – флуктуации (возмущения, небольшие отклонения) плотности и скорости вещества в пространстве под действием сил тяготения. Гравитационная неустойчивость является причиной возникновения галактик, звезд и звездных скоплений.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задачи на закон всемирного тяготения с решениями

Хотите узнать, как решать задачи на закон всемирного тяготения? Вот памятка по решению любых задач и отдельная статья про задачи на движение тел под действием силы тяжести.

Задача №1. Применение закона всемирного тяготения

Условие

Два одинаковых шара притягиваются друг к другу с силой 6,67*10^-5 Ньютона. Масса каждого шара равна 20 тонн. Найдите расстояние между шарами.

Решение

По закону всемирного тяготения

Ответ: 20 метров.

Задача №2. Расчет ускорения свободного падения на Марсе

Условие

Каково ускорение свободного падения на Марсе?

Решение

Сначала по справочнику найдем значения массы и радиуса Марса:

По закону всемирного тяготения для тела массы m на Марсе:

Сократим m и получим формулу для ускорения свободного падения:

Ответ: 3,72 метра на секунду в квадрате.

Задача №3. Нахождение первой космической скорости на поверхности Луны

Условие

Какова первая космическая скорость на поверхности Луны?

Решение

Первая космическая скорость у поверхности планеты находится по формуле:

Также из этой задачи можно найти ускорение свободного падения на Луне. Оно равно 1,61 м/с2.

Ответ: 1,7 км/с.

Задача №4. Изменение ускорения свободного падения с четом высоты

Условие

Воздушный шар поднимается на высоту 6 километров. Как изменится ускорение свободного падения на этой высоте?

Решение

Запишем закон всемирного тяготения сначала для поверхности Земли, а потом для высоты h. Обозначим ускорение свободного падения на уровне моря как g нулевое.

Ответ: Ускорение свободного падения уменьшится на 0,02 м/с2.

Задача №5. Применение закона всемирного тяготения

Условие

Определите, какая из сил притяжения больше: сила между Землей и Луной или сила между Луной и Солнцем

Решение

Чтобы понять, какая сила больше, нужно их сравнить.

Учитывая, что расстояние между Землей и Луной гораздо меньше, чем расстояние межу Землей и Солнцем, вместо расстояния между Луной и Солнцем можно взять расстояние Земля-Солнце.

Ответ: сила притяжения между Луной и Солнцем примерно в два раза больше.

Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.

Источник