Составным числом называется такое натуральное число которое
Составные числа
Любое натуральное число больше единицы является либо простым либо составным. Простым называют число, которое делится без остатка только на само себя или на единицу (2, 3, 5, 7 и т.д.). Составным называется число, которое имеет больше двух делителей (4, 6, 8 и т.д.).
Таблица составных чисел до 100
| 4 | 6 | 8 | 9 | 10 | 12 | 14 | 15 | 16 | 18 | 20 | 21 |
| 22 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 33 | 34 | 35 | 36 |
| 38 | 39 | 40 | 42 | 44 | 45 | 46 | 48 | 49 | 50 | 51 | 52 |
| 54 | 55 | 56 | 57 | 58 | 60 | 62 | 63 | 64 | 65 | 66 | 68 |
| 69 | 70 | 72 | 74 | 75 | 76 | 77 | 78 | 80 | 81 | 82 | 84 |
| 85 | 86 | 87 | 88 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 98 |
| 99 | 100 |
Самое маленькое составное число
Исходя из определения и пользуясь таблицей составных чисел, видно, что наименьшее натуральное составное число — 4.
Важно! Единица — не является ни простым, ни составным числом
Как определить составное ли число?
Возвращаясь к определению, получаем, что если число делиться без остатка на любое число, кроме самого себя и единицы — значит оно составное. Проверить это можно путем перебора делителей (к примеру, начать делить на 2, затем на 3 и т.д.), либо зная признаки делимости.
Простые и составные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Простые числа. Составные числа
Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.
Другими словами число является простым, если имеет только два различных натуральных делителя.
Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.
Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.
Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.
Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку «Создать» и подождите несколько секунд.
Таблица простых чисел
Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.
Если k1 число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p2, что
Если k2 число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:
Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).
Допустим существует два разложения числа k:
Так как k=p1p2p3. делится на простое число q1, то по крайней мере один из множителей, например p1 делится на q1. Но p1 простое число и делится только на 1 и на себя. Следовательно p1=q1 (т.к. q1≠1)
Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■
Разложение составного числа k можно записать в следующем виде
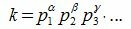 | (3) |
Разложение (3) называется каноническим разложением числа.
Теорема 2. Количество простых чисел бесконечно много.
Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:
Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.
Данная теорема является частным случаем более общей теоремы:
Теорема 3. Пусть задана арифметическая прогрессия
где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.
Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.
Число и сумма всех делителей числа
Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.
Если m делится на n, то n является кратным m:
Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.
Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.
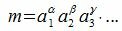 |
Тогда все делители n числа m можно представить формулой
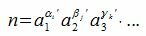 | (6) |
Каждая из чисел n вычисленная формулой (6) является делителем числа m.
Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:
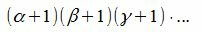 |
Мы доказали следующую теорему:
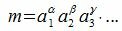 |
каноническое разложение числа m. Тогда число делителей числа m равно:
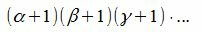 |
Составим все произведения вида 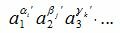
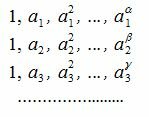 |
Тогда для произведения вида 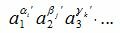
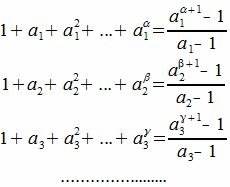 |
Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.
Следовательно сумма всех делителей числа m равна
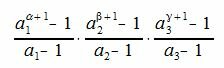 | (7) |
Мы доказали следующую теорему:
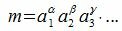 |
каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).
Какие числа называют составными в математике
Составные числа — понятие и определение
Такие числа, которые используют при счете объектов и предметов, называют натуральными.
Натуральные числа бывают простыми и составными.
Если у числа есть только два делителя — единица и само число — то его называют простым. Самое маленькое простое число — это 2.
Например, к простым относят также 3, 5 и 7.
У 3 есть только два делителя: 1 и 3.
Составные числа являются натуральными и имеют больше двух делителей.
Например, 125 делится на 1, 5, 25, 125. Это составное число.
Единица не относится ни к простым, ни к составным натуральным числам.
Делителем числа называют такое число, при делении на которое полученный результат является целым (не имеет остатка).
Нельзя назвать самое большое составное число, потому что их бесконечное множество. Но можно определить самое маленькое натуральное составное число — это 4.
Чем отличаются от простых
Составные числа отличаются от простых тем, что у них есть еще хотя бы один делитель, который не равен единице и самому числу. Простое число имеет только два делителя: единицу и само себя.
С помощью нахождения делителей определяют, является ли число простым или составным. Чтобы найти делители числа, нужно разложить его на множители.
Разложить число на множители — значит, представить его в виде произведения чисел.
Множители подбирают с помощью применения признаков делимости, а также разложения числа на простые множители.
Разложение на простые множители — это математическая операция, которая представляет число в виде произведения простых множителей.
Основная теорема арифметики:
Любое составное число можно разложить на простые множители (представить в виде произведения) единственным способом.
Применение составных чисел
Каждое составное число в математике представляют в виде произведения двух и более натуральных чисел, которые больше единицы.
Составные числа встречаются повсюду:
Числа позволяют создавать математические модели, с опорой на которые принимаются актуальные решения.
Примеры решения задач
Найдите среди чисел 16, 37, 11, 58 и 13 составные.
По определению, число является составным, если оно имеет хотя бы один делитель, кроме 1 и самого себя.
16 делится нацело, например, на 2 и 8, значит, 16 является составным.
37 можно найти в таблице простых чисел.
| 2 | 79 | 191 | 311 | 439 | 577 | 709 | 857 |
| 3 | 83 | 193 | 313 | 443 | 587 | 719 | 859 |
| 5 | 89 | 197 | 317 | 449 | 593 | 727 | 863 |
| 7 | 97 | 199 | 331 | 457 | 599 | 733 | 877 |
| 11 | 101 | 211 | 337 | 461 | 601 | 739 | 881 |
| 13 | 103 | 223 | 347 | 463 | 607 | 743 | 883 |
| 17 | 107 | 227 | 349 | 467 | 613 | 751 | 887 |
| 19 | 109 | 229 | 353 | 479 | 617 | 757 | 907 |
| 23 | 113 | 233 | 359 | 487 | 619 | 761 | 911 |
| 29 | 127 | 239 | 367 | 491 | 631 | 769 | 919 |
| 31 | 131 | 241 | 373 | 499 | 641 | 773 | 929 |
| 37 | 137 | 251 | 379 | 503 | 643 | 787 | 937 |
| 41 | 139 | 257 | 383 | 509 | 647 | 797 | 941 |
| 43 | 149 | 263 | 389 | 521 | 653 | 809 | 947 |
| 47 | 151 | 269 | 397 | 523 | 659 | 811 | 953 |
| 53 | 157 | 271 | 401 | 541 | 661 | 821 | 967 |
| 59 | 163 | 277 | 409 | 547 | 673 | 823 | 971 |
| 61 | 167 | 281 | 419 | 557 | 677 | 827 | 977 |
| 67 | 173 | 283 | 421 | 563 | 683 | 829 | 983 |
| 71 | 179 | 293 | 431 | 569 | 691 | 839 | 991 |
| 73 | 181 | 307 | 433 | 571 | 701 | 853 | 997 |
Число 11 также найдем в таблице простых чисел.
58 можно разделить на 2, так как по признаку делимости, если число оканчивается четной цифрой, то оно делится нацело на 2. Значит, число имеет делитель, который отличается от 1 и 58. Следовательно, 58 — составное.
13 находим в таблице простых чисел.
Докажите, что число 296 является составным.
Число является составным, если у него есть хотя бы один делитель, кроме единицы и самого себя.
Для нахождения делителя, используем признаки делимости.
296 заканчивается на 6. Цифра 6 — четная, значит, по признаку делимости число делится без остатка на 2. И, если у него есть хотя бы один делитель, кроме 1 и 296 (в данном случае это 2), то оно является составным.
Что и требовалось доказать.
Можно ли говорить о том, что все четные числа являются составными?
Ответ: нет, так как, например, число 2 является четным, но при этом простым, потому что имеет только два делителя — 1 и 2.
Приведите примеры четырех составных чисел, кратных 3.
Числа, которые кратны трем, делятся на 3 нацело.
Вспоминаем признак делимости на 3: сумма цифр числа должна делиться нацело на 3.
Тогда нужными нам примерами могут быть: 27, 126, 45 и 99.
27: составное число, так как имеет хотя бы один делитель, кроме 1 и самого себя — это 3. Сумма цифр числа равняется 9. Девять кратно 3.
126: составное, так как делится нацело на 2 — в разряде единиц стоит четная цифра 6. Сумма цифр — 1 + 2 + 6 = 9 — 9 кратно 3.
45: составное, делится нацело на 5 по признаку делимости. Сумма цифр равна 9, девять кратно 3.
99: составное, так как делится нацело на 9 по признаку делимости. Сумма цифр равна 18, а 18 кратно 3.







