Соедини точки так чтобы получилась незамкнутая ломаная
Математика 1 класс учебник 2 часть ответы стр 41
👉 Ответы к странице 41. Математика 1 класс учебник 2 часть. Авторы: М. И. Моро, С. И. Волкова.
Выпиши примеры, в решении которых допущена ошибка.
У Гали две собаки: одной 10 лет, а другой 2 года. Узнай, на сколько лет одна из них старше другой.
Составь и реши задачу, в условии которой есть слово больше.
Задача. У Димы 5 рублей, а у Миши на 2 рубля больше. Сколько у Миши рублей?
Составь и реши задачу, в вопросе которой есть слово меньше.
У Миши было 10 конфет, а у Димы на 5 конфет меньше. Сколько у Димы конфет? 10 — 5 = 5 конфет.
Мама сварила варенье и разлила его в 2 банки, по 3 л в каждую.
Поставь вопрос и реши задачу.
Вопрос. Сколько всего варенья сварила мама?
Мама сварила 6 кг варенья
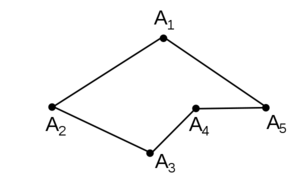
Отметь в тетради точки, как на рисунках
Соедини точки отрезками так, чтобы на первом рисунке получилась ломаная из трёх звеньев, а на втором — ломаная из четырёх звеньев. Чем вторая ломаная отличается от первой? Как её можно назвать по-другому?
Не вычисляя, найди лишний пример.
Лишний пример 3 + 3
Все примеры на вычитание и только один на сложение.
Списать «Проверочные работы», перейти на страницу 34
Математика 1 класс учебник Моро 1 часть страница 42
👉 Ответы на задания к странице 42. Математика 1 класс учебник Моро 1 часть. Моро М. И, Волкова В. С.
✔ Готовое домашнее задание с подробным решением
Ломаная линия
Найди на чертеже ломаную. Объясни свой выбор.
2 вариант — ломаная линия.
Ломаные линии составлены из отрезков. У ломаной линии конец одного отрезка — начало другого, кроме концов ломаной.
Первый вариант не подходит, потому что присутствуют кривые линии. У ломаной линии отрезки прямые.
Второй вариант — ломаная линия. Отрезки не принадлежат одной прямой и из конца следующего отрезка выходит новый отрезок.
Третий вариант не подходит, потому что это прямая линия — все отрезки лежат на одной прямой.
Начерти в тетради ломаную из трех звеньев. Сколько у нее вершин? Начерти ломаную из трех звеньев с тремя вершинами. Какая фигура получилась?
У нарисованной ломаной 2 вершины.
У нарисованной ломаной 3 вершины. Получился треугольник.
Задание 3. Задание на полях.
У верхних фигур количество вершин и звеньев разные, а у нижних фигур количество вершин и звеньев одинаковое.
На первом изображении у красной фигуры 5 звеньев; у синей фигуры 4 звенья.
На втором изображении у зеленой фигуры 4 звенья; у оранжевой фигуры 5 звеньев.
На первом изображении у красной фигуры 4 вершины; у синей 3 вершины.
На втором изображении у зеленой фигуры 4 вершины; у оранжевой фигуры 5 вершин.
💡 Чтобы не искать ГДЗ к упражнениям в следующий раз сохрани в закладки. Нажми на клавиатуре CTRL + D или поделись в социальных сетях.
Присоединяйтесь к нам!
Получайте уведомления о выходе новых решебников и примите участие в ежемесячном розыгрыше.
Математика 1 класс учебник Моро 1 часть страница 42
👉 Ответы к странице 42. Математика 1 класс учебник 1 часть. Авторы: М. И. Моро, С. И. Волкова.
Ломаная линия
Найди на чертеже ломаную. Объясни свой выбор.
Ломанная линия отмечена цифрой 2.
Первый вариант не подходит, потому что в ней есть кривые линии, а в ломанной только прямые.
Второй вариант подходит, потому что отрезки не принадлежат одной прямой и из конца следующего выходит новый отрезок.
Третий вариант похож на прямую, так как все отрезки лежат на одной прямой.
Начерти в тетради ломаную из трёх звеньев. Сколько у неё вершин? Начерти ломаную из трёх звеньев с тремя вершинами. Какая фигура получилась?
У нарисованной ломанной 2 вершины.
На первой картинке, которая изображена сверху, у красной фигуры 4 вершины и 5 звеньев. У синей фигуры 3 вершины и 4 звена.
На втором рисунке, который изображен снизу, у зеленой фигуры 4 вершины и 4 звена. У оранжевой фигуры 5 вершин и 5 звеньев.
В итоге можно сделать вывод, что у верхних фигур количество вершин и звеньев разное, а у нижних фигур количество вершин и звеньев совпадает.
Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
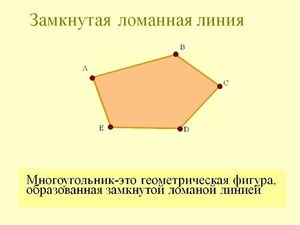
Как выглядит замкнутая ломаная линия
Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.
Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.
Особенности замкнутых линий
Рассмотрим подробнее составляющие части этой геометрической фигуры.
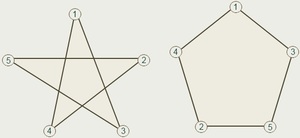
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.
Многоугольник как разновидность замкнутой ломаной
Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.
Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.
Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.
У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.
Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.
Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.