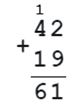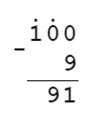Соедини точки отрезками так чтобы получился пятиугольник сделай это двумя разными способами
Правильный пятиугольник — построение, свойства и формулы
Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.
Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:
Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:
Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:
Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:
Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.
Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).
Соотношения и формулы
После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:
Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:
Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:
Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:
Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.
Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 1 Страница 99-106
Страница 99
Страница 100
2. Объясни, как сделаны записи.
2 • 2 = 4 2 • 3 = 6 2 • 4 = 8
Ответ:
Количество фишек в одном ряду умножили на количество рядов:
На 1 рисунке: 2 фишки в одном ряду умножили на 2 ряда получили 4 фишки.
На 2 рисунке: 2 фишки в одну ряду умножили на 3 ряда получили 6 фишек.
На 3 рисунке: 2 фишки в одном ряду умножили на 4 ряда получили 8 фишек.
3. Сколько рядов с двумя фишками надо взять, чтобы умножить 2 на 0?
Сколько фишек должно быть в ряду, чтобы умножить 0 на 2? Какой результат получится, если взять это число фишек два раза?
Ответ:
Чтобы умножить 2 на 0, нужно взять 0 рядов по 2 фишки (2 • 0 = 0).
Чтобы умножить 0 на 2, должно быть 2 ряда по 0 фишек (0 • 2 = 0).
Если взять 0 фишек два раза, то получится 0 (0 • 0 = 0).
4. Найди результаты умножения.
2 • 5 2 • 8
2 • 6 2 • 9
2 • 7 2 • 4
Ответ:
2 • 5 = 10
2 • 6 = 12
2 • 7 = 14
2 • 8 = 16
2 • 9 = 18
2 • 4 = 8
5. Сравни результаты умножения, используя калькулятор.
2 • 6 и 6 • 2 3 • 2 и 2 • 3
9 • 2 и 2 • 9 2 • 1 и 1 • 2
Сделай вывод.
Ответ:
2 • 6 = 12 6 • 2 = 12
9 • 2 = 18 2 • 9 = 18
3 • 2 = 6 2 • 3 = 6
2 • 1 = 2 1 • 2 = 2
Можно сделать вывод, что от перемены мест множителей произведение не меняется.
6. Используя таблицу умножения числа 2, составь и запиши таблицу умножения на число 2.
Ответ:
2 • 1 = 2
2 • 2 = 4
2 • 3 = 6
2 • 4 = 8
2 • 5 = 10
2 • 6 = 12
2 • 7 = 14
2 • 8 = 16
2 • 9 = 18
2 • 10 = 20
7. Назови результаты умножения.
6 • 2 4 • 2 7 • 2 9 • 2
8 • 2 3 • 2 1 • 2 5 • 2
Ответ:
6 • 2 = 12
8 • 2 = 16
4 • 2 = 8
3 • 2 = 6
7 • 2 = 14
1 • 2 = 2
9 • 2 = 18
5 • 2 = 10
Страница 101
12. На сколько квадратов разделён каждый четырёхугольник? Посчитай разными способами.
Ответ:
Желтый четырехугольник.
1 способ: 1 + 1 + 1 + 1 + 1 + 1 = 6 квадратов
2 способ: 2 + 2 + 2 = 6 квадратов
3 способ: 3 + 3 = 6 квадратов
4 способ: 2 • 3 = 6 квадратов
5 способ: 3 • 2 = 6 квадратов
Зеленый четырехугольник.
1 способ: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 18 квадратов
2 способ: 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 квадратов
3 способ: 9 + 9 = 18 квадратов
4 способ: 2 • 9 = 18 квадратов
5 способ: 9 • 2 = 18 квадратов
13. Используя таблицу умножения на 2, выполни деление.
6 : 2 14 : 2 4 : 2 12 : 2
10 : 2 16 : 2 8 : 2 18 : 2
Ответ:
6 : 2 = 3
10 : 2 = 5
14 : 2 = 7
16 : 2 = 8
4 : 2 = 2
8 : 2 = 4
12 : 2 = 6
18 : 2 = 9
Страница 102
14. Выполни действия.
6 • 2 2 • 8 7 • 2 9 • 2
12 : 2 16 : 2 14 : 2 18 : 2
Ответ:
6 • 2 = 12
12 : 2 = 6
2 • 8 = 16
16 : 2 = 8
7 • 2 = 14
14 : 2 = 7
9 • 2 = 18
18 : 2 = 9
15. Какое число получится, если умножить 0 на 2 и разделить результат на 2?
Ответ:
0 • 2 = 0 0 : 2 = 0
Страница 103
Страница 104
25. Катя хочет надеть на куклу блузку и юбку. Сколько разных костюмов она может составить, если имеется 2 юбки и 3 блузки?
Действуй по плану.
1) Выбери одну из двух юбок и присоединяй к ней по порядку каждую из трёх блузок.
2) Ко второй юбке присоединяй по порядку каждую из трёх блузок.
Проверь своё решение: всего должно получиться 6 костюмов.
Ответ:
1) Юбка в складку и бело-зеленая блузка, юбка в складку и белая в розовую полоску блузка, юбка в складку и желтая с цветами блузка.
2) Джинсовая юбка и бело-зеленая блузка, джинсовая юбка и белая в розовую полоску блузка, джинсовая юбка и желтая с цветами блузка.
Да, всего получится 6 костюмов.
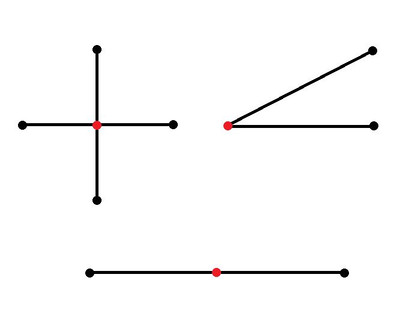
26. Начерти два отрезка так, чтобы их общей частью была точка. Рассмотри разные варианты расположения отрезков.
Ответ:
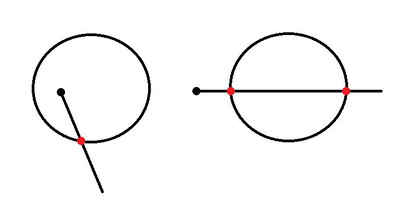
27. Начерти окружность и луч так, чтобы луч пересекал эту окружность в одной точке; в двух точках.
Ответ:
Страница 105.
28. Миша говорит, что он начертил отрезки, симметричные относительно оси. Верно ли Миша выполнил чертёж?
Ответ:
Если перегнуть лист по оси (красной линии), то отрезки должны совпасть. В данном случае отрезки не совпадут, а будут параллельны друг другу. Поэтому Миша выполнил чертеж не верно.
29. Начерти какую-нибудь окружность с центром в точке О. Отметь три точки: точку К — вне окружности, точку В — на окружности и точку М — внутри окружности. Построй отрезки ОК, ОВ и ОМ. Не производя измерений, сравни длины отрезков ОК и ОВ, ОК и ОМ, ОВ и ОМ. Свои ответы поясни.
Ответ: 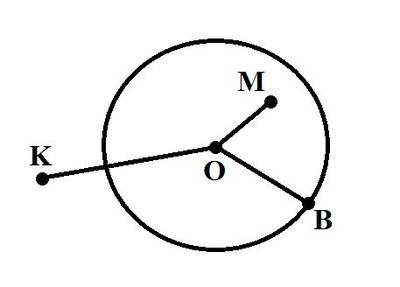
Отрезок OB находится на окружности, т.е. является ее радиусом, а отрезок OK находится за пределами окружности, поэтому ОК>ОВ
Отрезок OK находится за пределами окружности, а отрезок OM внутри окружности, поэтому ОК>ОМ
Отрезок OB равен радиусу, а отрезок OM внутри окружности, т.е. меньше радиуса, поэтому ОВ>ОМ
30. Найди неизвестные числа.
Число 42 меньше неизвестного числа на 19. Чему равно неизвестное число?
Число 63 больше неизвестного числа на 24. Чему равно неизвестное число?
Коля задумал двузначное число. В нём 10 десятков без 9 единиц. Какое это число?
Ответ:
Число 42 меньше неизвестного числа на 19. Чему равно неизвестное число?
Число 63 больше неизвестного числа на 24. Чему равно неизвестное число?
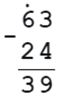
Коля задумал двузначное число. В нём 10 десятков без 9 единиц. Какое это число?
10 десятков = 100
9 единиц = 9
А 10 десятков без 9 единиц, т.е. надо из 100 вычесть 9
Страница 106
33. Составь цепочку из пяти чисел: первое число 15, а каждое следующее на 20 больше предыдущего.
Ответ:
15 + 20 = 35 35 + 20 = 55 55 + 20 = 75 75 + 20 = 95
Цепочка: 15, 35, 55, 75, 95
34. Не отрывая карандаша от бумаги и не проводя два раза одну и ту же линию, обведи каждую фигуру.
Ответ:
35. Начерти какой-нибудь четырёхугольник. Проведи отрезок так, чтобы он разделил данный четырёхугольник:
1) на два треугольника;
2) на треугольник и четырёхугольник.
Ответ: 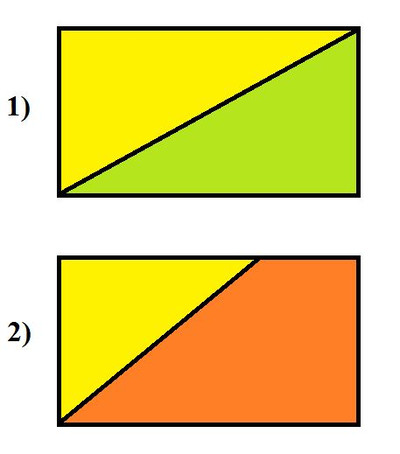
36. Измерь длины сторон многоугольников и найди периметры этих фигур двумя способами.
Ответ:
37. Начерти от руки треугольник, квадрат, круг, пятиугольник.
Ответ:
Самостоятельное выполнение
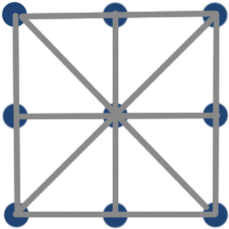
Соединить 9 точек чтобы получить многоугольник

Оглавление:
Условие задачи
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
Эта задача является не такой уж простой, как может показаться. Чтобы ее решить нужно думать нестандартно и применить свое творческое мышление, иначе ничего не получится. Если пытаться действовать в лоб начать соединять все точки стандартными линиями, то вы можете потратить уйму времени и так и не решить задачу девяти точек. Наше стандартное мышление, которому нас учат в школе, направляет нас искать решение, опираясь лишь на шесть типичных линий: 4 стороны квадрата и 2 его диагонали. Большинству людей кажется, что решение головоломки о 9 точках должно лежать именно в этих рамках. Но его там нет. Его даже не найти если подключить еще 2 линии между центрами сторон квадрата:
Вообще между всеми девятью точками можно провести всего 20 прямых линий: 4 стороны квадрата; 2 диагонали; 6 линий, соединяющих центры сторон большого квадрата; 8 линий соединяющих центры сторон большого квадрата с его углами. Как нарисовать все отрезки, соединяющие наши 9 точек, показано на рисунке ниже:
Но, даже используя эту схему, невозможно найти 4 линии, которыми можно было бы соединить все девять точек, не отрывая руки.
Верное решение «теста 9 точек»
Решение этой головоломки лежит несколько шире нашего стандартного восприятия задачи. Для того, чтобы самостоятельно найти верный подход вспомните, что:
Таким образом, давайте попробуем продолжить линии за пределы, ограничивающего нас до недавнего времени квадрата. Тут видно, что область нашего поиска значительно увеличилась. Потрудившись немного можно прийти к одному из правильных решений.
Последовательность соединений девяти точек четырьмя линиями:
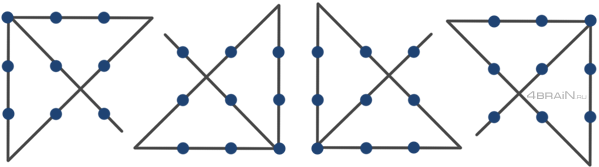
Другие варианты. Этот способ не единственный, начинать можно от любого угла и двигаться одном из двух направлений. На сайте 4brain таких вариантов решения задачи «9 точек 4 линии» представлено минимум 12:
Только подумайте, задача, которую многие никак не могут решить, имеет 12 способов решения. Также смотрите упрощенный вариант этой задачи: как соединить 4 точки тремя линиями, чтобы линии замыкались в целую фигуру.
Творческий подход в этой головоломке
Большинство людей, которые решали эту задачу, так и не смогли выбраться за рамки стандартного мышления, которое в данном тесте выражено квадратом, образованным девятью точками. Нам комфортно смотреть на любую жизненную задачу прямо, наиболее просто. С другой стороны, человек может потратить много времени и сил для того, чтобы, используя стандартный подход, найти верное решение, когда это решение лучше искать, изначально подойдя к процессу творчески.
В нашей жизни мы часто сталкиваемся с такими задачами о «девяти точках и четырех линиях», и для того, чтобы их решать развивайте свое креативное мышление, в том числе и при помощи нашего тренинга. Ведь задача о 9 точках имеет и другие решения (об этом читайте дальше).
Другие способы решения
Изменив наш фрейм или применив латеральный разрыв можно найти и другие варианты решения этой задачи. Например, метод гиперболизации при создании латерального разрыва может нас привести к мысли, что никто не уточняет, что в задаче должны применяться стандартные условия геометрии (о бесконечной малости точек и бесконечной тонкости линий). Пусть наша линия будет настолько широкой, что сможет сразу пересекать несколько точек по своей ширине. Тогда мы не то что 4-мя линиями сможем соединить все 9 точек, а даже одной.
Кроме того, даже в нашем изображении 4-х точек, которое дано в нашем условии головоломки о 9 точках, сами точки-кружки достаточно большие, чтобы можно было их соединить 3-мя линиями вот так:
А может вообще не стоит ограничиваться двухмерным пространством или использовать концепцию искривления пространства. Также мы можем акцентировать внимание на фразу «не отрывая ручки от листа бумаги», и просто положив ручку на бок передвинуть ее и таким образом нарисовать просто 3 параллельных линии.
Нестандартная по своему рассуждению задачка о том, как соединить 9 точек 4 линиями, заставляет разбить стереотипы и включить творчество.
Как правильно расположить точки и рисунок?
На листе бумаги, лучше если он будет в клеточку, нужно нарисовать 9 точек. Они должны быть расположены по три в ряд. Выглядеть схема будет, как квадратик, в центре которого стоит точка, и посередине каждой из сторон тоже она имеется. Лучше, если этот рисунок расположить в стороне от краев листа. Такое размещение квадратика потребуется для того, чтобы правильно решить задачу о том, как соединить 9 точек 4 линиями.
Условие задачи
Требования, которые обязательно нужно учесть:
Соблюдая эти правила, нужно соединить 9 точек 4 линиями. Очень часто уже через пару минут размышлений над этим рисунком человек начинает утверждать, что ответа у этого задания нет.
Решение задачи
Главное в том, чтобы забыть все, чему учили в школе. Там дают стереотипные представления, которые здесь только помешают.
Основная причина того, что задание о том, как соединить 9 точек 4 линиями, не разгадывается в следующем случае: они заканчиваются в нарисованных точках.
Это принципиально неправильно. Точки — это концы отрезков, а в задаче явно говорится о линиях. Этим и нужно обязательно воспользоваться.
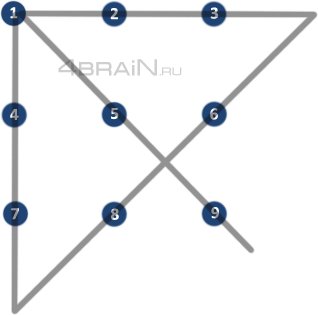
Начинать можно с любой вершины квадрата. Главное, именно угол, какой конкретно, не принципиально. Пусть обозначены точки будут слева, двигаясь направо, и сверху, перемещаясь вниз. То есть в первом ряду находятся 1, 2 и 3, второй состоит из 4, 5 и 6, а третий образован 7, 8 и 9.
Пусть начало будет находиться в первой точке. Тогда, чтобы соединить 9 точек 4 линиями, потребуется выполнить следующее.
На этом задание завершено и все условия соблюдены. Кому-то эта фигура напоминает зонт, а кто-то утверждает, что она — стрелка.
Если записать короче план того, как соединить 9 точек 4 линиями, то получится следующее: начать в 1, продолжить в 5, поворот в 9, провести в 6 и 3, продлить до (0), повернуть на 2 и 4, продолжить до (0), свернуть к 7, 8 и 9. Здесь (0) обозначены концы отрезков, у которых нет цифр.
В качестве заключения
Теперь можно еще поломать голову над более сложной задачкой. В ней уже 16 точек, расположенных аналогично рассмотренному заданию. И соединить их нужно уже 6 линиями.
Если и это задание оказалось по зубам, то можно попытаться решить другие, с такими же требованиями, но отличающиеся набором точек и прямых, из следующего списка:
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Многоугольник – это замкнутая линия, которая образовывается, если взять каких-либо точек и соединить их последовательно отрезками.
При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).
Многоугольник с сторонами называют -угольником.
Произвольные многоугольники
Давай-ка нарисуем, какие бывают многоугольники.
А теперь вопрос: какой из этих многоугольников выпадает из ряда?
Посмотри внимательно на второй многоугольник – он по-существу отличается от всех остальных. Чем же? Он не выпуклый. Это конечно математическое название, но с человеческой интуицией не расходится.
Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.
Итак, основной факт:
Давай сразу к примерам:
Четырехугольник
 |
Пятиугольник
 |
Шестиугольник
 |
Ах да, про треугольник забыли.
Треугольник
 |
Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:
 | Всего вершин: Из вершины можем провести диагонали во все вершины, кроме: |
| Сумма углов многоугольника равна |
Что же из этого может оказаться полезным? А вот что:
Правильные многоугольники
| Многоугольник называется правильным, если все его углы и все его стороны равны. |
Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.
Первый вопрос:
А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?
И ответ: можно!
Давай посмотрим на примере.
Пусть есть, скажем, правильный восьмиугольник:
Значит любой угол, скажем можно найти:
Что мы еще должны знать?
| Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность. |
При этом центры этих окружностей совпадают.
Смотри как это выглядит!
И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.
Значит, – и это не только в восьмиугольнике!
И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.
МНОГОУГОЛЬНИКИ. КОРОТКО О ГЛАВНОМ
Многоугольник – это замкнутая линия, которая образовывается, если взять каких-либо точек и соединить их последовательно отрезками.
Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.
Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике,
А также получить доступ к учебнику YouClever без ограничений.