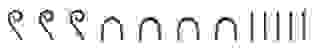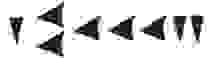Семеричная система счисления что это
Основы систем счисления
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32: 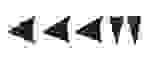
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92: 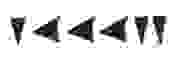
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа: 
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Q n (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Пример: 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Циклы времени Часть 4. Известные системы счисления. (ч. 2)
Прежде знак M изображался знаком Ф. Поэтому 500 стал изображать знак D, как «половина» Ф. Так же построены и пары L и C, X и V.
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.
CCXXXVII = 100+100+10+10+10+5+1+1 = 237; XXXIX = 10+10+10-1+10 = 39
Есть правило, по которому нельзя записывать подряд 4 одинаковых цифры, такая комбинация заменяется комбинацией с правилом вычитания, например:
Позиционная или мультипликативная система счисления — система счисления, в которой вес цифры меняется с изменением положения цифры в числе и определяется написанием цифры и местом, которое она занимает.
Вавилонская клинописная система счисления считается первой известной нам позиционной системой счисления. Согласно ОИ, использовалась еще на заре человеческой цивилизации – в III тысячелетии до нашей эры. Она сочетала три основания – 1, 10 и 60.
Для чисел от 1 до 9 использовались вертикальные клинья (палочки), как в единичной системе счисления. Для сокращения записи использовался угловой клин, заменявший 10 вертикальных. Угловой клин можно было повторять до 5 раз, а вместо 6 угловых клиньев вновь писался вертикальный, но перед ними. Тем самым наборы от 1 до 9 вертикальных и от 1 до 5 угловых клиньев превращались в цифры (десятичные и шестидесятеричные).
Еще один специальный символ, аналог нуля, использовался для указания пропуска пустых разрядов, то есть для обозначения границы между шестидесятеричными классами, но лишь в тех случаях, когда без него запись числа могла бы стать двусмысленной.
Шестидесятеричная система счисления появилась у вавилонян позже десятеричной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор ученые спорят, когда и как возникла у вавилонян шестидесятеричная система. На этот счет строилось множество гипотез, но ни одна не доказана.
Шестидесятеричная система счисления.
Ведет свою историю с Древнего Египта, то есть с IV тысячелетия до нашей эры. Ее появление вызвано сочетанием двух причин.
Во-первых, при счете на пальцах можно фиксировать до 60 различных положений косточек или суставов между ними.
Во-вторых, 60 лет – наименьшее общее кратное периодов обращения вокруг Солнца всех планет Солнечной системы, доступных для наблюдения без оптических приборов. Поэтому именно 60 лет были периодом, на который составлялись древние астрономические календари.
Суть другой гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60. Отголоски использования этой системы счисления дошли до наших дней. Например, 1 час = 60 минут, 1 градус = 60 минут.
Шестидесятеричная система счисления до сих пор сохранилась в измерении углов и времени. Угол равностороннего треугольника делится на 60 градусов. Градус, как и час, делится на 60 минут, а минута – на 60 секунд.
Шестидесятилетний цикл летоисчисления широко известен, как восточный календарь, в двух вариантах – японском и китайском.
Двенадцатеричная система счисления.
На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов. В русском языке счет часто идет дюжинами.
Семеричная Система счисления.
В славянской десятичной системе счисления буквам старой славянской азбуки были присвоены цифровые значения: от 1 до 10, затем через 10 до 100 и через 100 до 1000.
Известно, что эта Славянская кириллическая нумерация была создана вместе со славянской алфавитной системой для славян греческими монахами братьями Кириллом (Константином) и Мефодием для переписки священных книг в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Если посмотреть внимательно, то увидим, что после «а» идет буква «в», а не «б» как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите. До XVII века эта форма записи чиcел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Интереснее всего записывались числа второго десятка:
В мультипликативной, позиционной системе счисления для записи чисел используется уже определенное количество цифр, которые могут принимать разные значения в зависимости от расположения в записи числа. Все цифры здесь изображаются определенными символами.
Например: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 11, 12, …, 99, 100, 101 …
Запись числа 1999 означает, что 1´ 1000 + 9 ´100 + 9 ´10 + 9. Для того, чтобы «собрать» такое число используется умножение (англ. multiplication ), из-за чего систему и назвали «мультипликативной».
Такие системы счисления были только у народов с очень хорошо развитой математикой. Такая система счисления годится для записи чисел и она очень удобна для счета. Любое из действий арифметики и алгебры может быть выполнено легко. Для счета здесь не нужна большая сноровка. По сей день мы используем только такую систему счисления.
Для мультипликативной системы нужно знать изображение цифр и их значение, а так же основание системы счисления. Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Если проще, то это число, с которого начинается второй разряд у числа. Для ныне используемых цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которых ровно 10, основанием нашей системы счисления будет 10. Система счисления называется » десятичная «.
Арабская нумерация – это самая распространенная на сегодняшний день нумерация.
Сегодня считается, что позиционная система записи чисел была изобретена в Индии «очень давно», затем была заимствована арабами, которые и занесли ее в средневековую Европу.
Поэтому название «арабская» для нее не совсем верно, поскольку хоть и завезли ее в Европу из арабских стран, но там она тоже была не родной. Настоящей родиной этой нумерации считается Индия.
В различных районах Индии существовали разнообразные системы нумерации, но в какой-то момент среди них выделилась одна.
Основная гипотеза А.Т. Фоменко и Г.В. Носовского (НХ) заключается в том, что современные арабские цифры произошли из славяно-греческих букв-цифр в XV – XVI веках Нашей Эры.
Конвертер величин
Определения единиц конвертера «Конвертер чисел в различных системах счисления.»
Двоичная система — позиционная система счисления с основанием 2. В этой системе числа записываются с помощью двух символов 0 и 1. Двоичная система используется во всех цифровых устройствах, таких как компьютеры и мобильные телефоны, так как ее проще всего реализовать в цифровой схемотехнике с помощью логических вентилей.
Пример: в двоичной системе двойка записывается как 10 и десять записывается как 1010.
Восьмеричная система — позиционная система счисления с основанием 8. В этой системе для записи любого числа используются символы 0–7.
Пример: в восьмеричной системе семерка записывается как 10 и шестьдесят шесть записывается как 100.
Десятичная система — позиционная система счисления с основанием 10. В этой системе для записи любого числа используются символы 0–9. Эта система наиболее широко использовалась во всех современных цивилизациях.
Шестнадцатеричная система — позиционная система счисления с основанием 16. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–F.
Пример: в шестнадцатеричной системе пятнадцать записывается как F и двести пятьдесят шесть записывается как 100.
Эта система широко используется в низкоуровневом программировании современных компьютеров, начиная с IBM System/360, аналогом которых в СССР были машины серии ЕС ЭВМ.
Двоичная система — позиционная система счисления с основанием 2. В этой системе числа записываются с помощью двух символов 0 и 1. Двоичная система используется во всех цифровых устройствах, таких как компьютеры и мобильные телефоны, так как ее проще всего реализовать в цифровой схемотехнике с помощью логических вентилей.
Пример: в двоичной системе двойка записывается как 10 и десять записывается как 1010.
Троичная система — позиционная система счисления с основанием 3. В этой системе числа записываются с помощью символов 0–2. Эта система используется в логике и в вычислительной технике реализуется с помощью устройств, имеющих три устойчивых состояния, например, высокий уровень, низкий уровень, неизвестное состояние (открытый выход или открытый коллектор).
Пример: в троичной системе тройка записывается как 10 и десять записывается как 101.
Четвертичная система — позиционная система счисления с основанием 4. В этой системе для записи любого числа используются символы 0–3.
Пример: в четвертичной системе четверка записывается как 10 и десять записывается как 22.
Пятеричная система — позиционная система счисления с основанием 5. В этой системе для записи любого числа используются символы 0–4.
Пример: в пятеричной системе пятерка записывается как 10 и двадцать пять записывается как 100.
Шестеричная система — позиционная система счисления с основанием 6. В этой системе для записи любого числа используются символы 0–5.
Пример: в шестеричной системе шестерка записывается как 10 и тридцать шесть записывается как 100.
Семеричная система — позиционная система счисления с основанием 7. В этой системе для записи любого числа используются символы 0–6.
Пример: в семеричной системе семерка записывается как 10 и сорок девять записывается как 100.
Восьмеричная система — позиционная система счисления с основанием 8. В этой системе для записи любого числа используются символы 0–7.
Пример: в восьмеричной системе восьмерка записывается как 10 и шестьдесят четыре записывается как 100.
Девятеричная система — позиционная система счисления с основанием 9. В этой системе для записи любого числа используются символы 0–8.
Пример: в девятеричной системе девятка записывается как 10 и восемьдесят один записывается как 100.
Десятичная система — позиционная система счисления с основанием 10. В этой системе для записи любого числа используются символы 0–9. Эта система наиболее широко использовалась во всех современных цивилизациях.
Одиннадцатеричная система — позиционная система счисления с основанием 11. В этой системе для записи любого числа используются цифры 0–9 и буква латинского алфавита A.
Пример: в одиннадцатеричной системе десятка записывается как A и сто двадцать один записывается как 100.
Двенадцатеричная система — позиционная система счисления с основанием 12. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–B.
Пример: в двенадцатеричной системе одиннадцать записывается как B и сто сорок четыре записывается как 100.
Тринадцатеричная система — позиционная система счисления с основанием 13. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–С.
Пример: в тринадцатеричной системе двенадцать записывается как С и сто шестьдесят девять записывается как 100.
Четырнадцатеричная система — позиционная система счисления с основанием 14. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–D.
Пример: в четырнадцатеричной системе тринадцать записывается как D и сто девяносто шесть записывается как 100.
Пятнадцатеричная система — позиционная система счисления с основанием 15. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–E.
Пример: в пятнадцатеричной системе четырнадцать записывается как E и двести двадцать пять записывается как 100.
Шестнадцатеричная система — позиционная система счисления с основанием 16. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–F.
Пример: в шестнадцатеричной системе пятнадцать записывается как F и двести пятьдесят шесть записывается как 100.
Эта система широко используется в низкоуровневом программировании современных компьютеров, начиная с IBM System/360, аналогом которых в СССР были машины серии ЕС ЭВМ.
Семнадцатеричная система — позиционная система счисления с основанием 17. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–G.
Пример: в семнадцатеричной системе шестнадцать записывается как G и семнадцать записывается как 10.
Восемнадцатеричная система — позиционная система счисления с основанием 18. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–H.
Пример: в восемнадцатеричной системе семнадцать записывается как H и восемнадцать записывается как 10.
Девятнадцатеричная система — позиционная система счисления с основанием 18. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–I.
Пример: в девятнадцатеричной системе восемнадцать записывается как I и девятнадцать записывается как 10.
Двадцатеричная система — позиционная система счисления с основанием 20. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–J.
Пример: в двадцатеричной системе девятнадцать записывается как J и четыреста записывается как 100.
В позиционной системе счисления с основанием 21 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–K.
Пример: в системе с основанием 21 десятичное число двадцать записывается как K и двадцать один записывается как 10.
В позиционной системе счисления с основанием 22 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–L.
Пример: в системе с основанием 22 десятичное число двадцать один записывается как L и двадцать два записывается как 10.
В позиционной системе счисления с основанием 23 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–M.
Пример: в системе с основанием 23 десятичное число двадцать два записывается как M и двадцать три записывается как 10.
В позиционной системе счисления с основанием 24 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–N.
Пример: в системе с основанием 24 десятичное число двадцать три записывается как N и двадцать четыре записывается как 10.
В позиционной системе счисления с основанием 25 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–O.
Пример: в системе с основанием 25 десятичное число двадцать четыре записывается как O и двадцать пять записывается как 10.
В позиционной системе счисления с основанием 26 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–P.
Пример: в системе с основанием 26 десятичное число двадцать пять записывается как P и двадцать шесть записывается как 10.
В позиционной системе счисления с основанием 27 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Q.
Пример: в системе с основанием 27 десятичное число двадцать шесть записывается как Q и двадцать семь записывается как 10.
В позиционной системе счисления с основанием 28 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–R.
Пример: в системе с основанием 28 десятичное число двадцать семь записывается как R и двадцать восемь записывается как 10.
В позиционной системе счисления с основанием 29 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–S.
Пример: в системе с основанием 29 десятичное число двадцать восемь записывается как S и двадцать девять записывается как 10.
В позиционной системе счисления с основанием 30 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–T.
Пример: в системе с основанием 30 десятичное число двадцать девять записывается как T и тридцать записывается как 10.
В позиционной системе счисления с основанием 31 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–U.
Пример: в системе с основанием 31 десятичное число тридцать записывается как U и тридцать один записывается как 10.
В позиционной системе счисления с основанием 32 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–V.
Пример: в системе с основанием 32 десятичное число тридцать один записывается как V и тридцать два записывается как 10.
В позиционной системе счисления с основанием 33 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–W.
Пример: в системе с основанием 33 десятичное число тридцать два записывается как W и тридцать три записывается как 10.
В позиционной системе счисления с основанием 34 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–X.
Пример: в системе с основанием 34 десятичное число тридцать три записывается как X и тридцать четыре записывается как 10.
В позиционной системе счисления с основанием 35 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Y.
Пример: в системе с основанием 35 десятичное число тридцать четыре записывается как Y и тридцать пять записывается как 10.
В позиционной системе счисления с основанием 36 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Z.
Пример: в системе с основанием 36 десятичное число тридцать пять записывается как Z и тридцать шесть записывается как 10.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Популярные конвертеры единиц
Конвертер чисел в различных системах счисления.
Позиционная система счисления (позиционная нумерация)— система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Основание 1 — единичная (унарная) система счисления; может рассматриваться как вырожденный случай позиционной системы счисления (счёт на пальцах, зарубки, узелки «на память» и др.);
Основание 2 — двоичная (в дискретной математике, информатике, программировании);
Основание 3 — троичная; иногда используется в вычислительной технике.
Основание 8 — восьмеричная;
Основание 10 — десятичная (используется повсеместно);
Основание 12 — двенадцатеричная (счёт дюжинами);
Основание 16 — шестнадцатеричная (используется в программировании, информатике);
Для записи чисел в системах счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0—9) и, затем, прописные или строчные буквы латинского алфавита (A—Z). При этом, a = 10, b = 11 и т. д.
Использование конвертера «Конвертер чисел в различных системах счисления.»
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!