найдите все натуральные nn такие что n3 1n3 1 является степенью возможно первой простого числа

Найдите все натуральные nn такие что n3 1n3 1 является степенью возможно первой простого числа

Ответ : 1; 3; 4; 8; 13; 28.

2.2. На шахматной доске построены векторы с началом в центре клетки С 2 (см. рисунок) и концами в центрах всех остальных клеток. Найдите модуль суммы этих векторов, если сторона клетки доски равна 1.

В такой системе координат центр каждой клетки имеет целочисленные координаты вида ( i ; j ) | –2 £ i £ 5; –1 £ j £ 6. Пусть сумма указанных векторов имеет координаты (а; b). Так как абсциссу и ординату суммы можно вычислять независимо друг от друга, то = 8 × 12 = 96; = 8 × 20 = 160.

Ответ : нет, не прав.

3.3. У Васи есть набор из 24 карандашей различных цветов. Он хочет раскрасить некоторое количество кругов по следующему правилу: каждый круг красится в три различных цвета, любое сочетание из двух цветов используется ровно один раз (то есть, если в каком-то круге встретились, например, красный и синий цвета, то ни в каком другом круге такое сочетание цветов невозможно) и каждое сочетание двух цветов должно быть использовано. Сможет ли он это сделать?

Ответ : нет, не сможет.

Предположим, что Вася смог раскрасить круги требуемым образом. Выберем один из использованных цветов и рассмотрим все круги в которых он присутствует. В каждом из этих кругов использовано еще по два цвета, причем все эти цвета – различны. Следовательно, их количество – четно. Это противоречит тому, что Васе требуется использовать еще 23 цвета.

4.3. Каждое из первых 2004 простых чисел возвели в степень, равную этому числу. Затем перемножили полученные числа и прибавили единицу. Является ли полученное число точным квадратом?

Ответ : нет, не является.

Заметим, что любое простое число, кроме числа 2, является нечетным. Нечетное число в любой натуральной степени – также нечетно, поэтому и их произведение является нечетным числом. Следовательно, полученное число можно записать в виде: 2 2 × (2 k + 1) + 1 = 8 k + 5, где k – некоторое натуральное число. Дальнейшие рассуждения можно провести различными способами.

5.3. На шахматной доске стоят десять белых фигур. Докажите, что можно поставить на эту доску черного коня так, чтобы он не нападал ни на одну из этих фигур.

Мысленно разобьем шахматную доску на четыре квадрата размером 4 ´ 4. Так как белых фигур – 10, то найдется квадрат, в котором стоит не более двух фигур. Без ограничения общности можно считать, что это левый верхний квадрат (см. рис. 6).

Источник

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Первый тур (10 минут; каждая задача – 6 баллов)

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Для каких значений x выполняется неравенство: ?

Ответ: для всех действительных значений x.

Первый способ. Оба слагаемых в левой части положительны. По неравенству между средним арифметическим и средним геометрическим .

Второй способ. Пусть > 0, > 0, тогда ab = = 2. Докажем, что . Предположим противное: a + b 4ab, то 4ab 0, кроме того, > 0, поэтому 0, то есть сумма любых семи чисел положительна.

3.2. Дан четырехугольник АВСD площади 1. Из его внутренней точки О опущены перпендикуляры OK, OL, OM и ON на стороны АВ, ВС, CD и DA соответственно. Известно, что AK ³ KB, BL ³ LC, CM ³ MD и DN ³ NA. Найдите площадь четырехугольника KLMN.

Из двух наклонных, проведенных из одной точки больше та, у которой проекция больше. Поэтому из неравенств, заданных в условии задачи, следует, что ОА ³ OB ³ OC ³ OD ³ OA. Значит, ОА = OB = OC = OD, то есть О – центр окружности, описанной около четырехугольника АВСD (см. рис. 2). Тогда точки K, L, M и N являются серединами сторон АВСD.

По теореме Вариньона (середины сторон четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника) получим, что .

3.3. В однокруговом турнире участвуют 10 шахматистов. Через какое наименьшее количество туров может оказаться так, что единоличный победитель уже выявился досрочно? (В каждом туре участники разбиваются на пары. Выигрыш – 1 очко; ничья – 0,5 очка; поражение – 0).

Ответ: через 7 туров.

Первый способ. Заметим, что после шестого тура разыграно 30 очков и у лидера – не более, чем 6 очков, тогда остальные девять участников в сумме набрали не менее, чем 24 очка. Следовательно, найдется хотя бы один шахматист, у которого более трех очков (по принципу Дирихле). Так как впереди еще 3 тура, то победитель пока неизвестен.

После 7 туров вполне могла сложиться ситуация, когда у лидера – 7 очков, а у каждого из остальных участников – меньше, чем 5 очков. Например, это возможно, если лидер свои партии выиграл, а все остальные партии закончились вничью. Тогда, у двух шахматистов, еще не игравших с лидером, – по 3,5 очка, а у других –по 3 очка. Так как до конца турнира осталось 2 тура, то в этом случае победитель уже определен.

Второй способ. Пусть после тура с номером m у лидера – n очков (n £ m), а у следующего за ним (возможно, не единственного) – k очков. К этому моменту разыграно 5m очков, значит все, кроме лидера, набрали в сумме 5m – n очков, поэтому . Тогда , но числа m и 2k – целые, а 0 6.

Построение примера описано выше.

Четвертый тур (25 минут; каждая задача – 9 баллов).

4.1. Числа x, y, z и t лежат в интервале (0, 1). Докажите неравенство:

0, b > 0 выполняется неравенство (следует из неравенства a2 + b2 a, то есть a 4. Из любой вершины графа выходит n – 4 ребра, а так как отношение дружбы транзитивно, то в графе есть полный подграф из n – 3 вершин. Для остальных вершин графа все вершины этого подграфа являются «врагами», поэтому n – 3 3, то есть n6. Таким образом, возможен только случай n = 6 (см. рис. 5).

Пятый тур (15 минут; каждая задача – 7 баллов).

5.1. На координатной плоскости изображен график функции y = ax2 + bx + c (см. рисунок). На этой же координатной плоскости схематически изобразите график функции y = cx2 + 2bx + a. Ответ поясните.

Вычислим значения a, b è c.

Первый способ. Выберем три удобные точки данного графика, например, (0; 1); (1; –2) и (–1; 2). Учитывая, что y(0) = c; y(1) = a + b + c; y(–1) = a – b + c, получим систему

уравнений: Ее решением является: a = –1; b = –2; c = 1.

Второй способ. Заметим, что данный график получается параллельным переносом графика функции y = –x2, поэтому a = –1. Значение b = –2 вычисляется из равенства (абсцисса вершины параболы), а с = y(0) = 1.

Следовательно, искомый график задается уравнением y = x2 – 4x – 1 Û y = (x – 2)2 – 5.

5.2. Верно ли, что в любом треугольнике точка пересечения медиан лежит внутри треугольника, образованного основаниями биссектрис?

Приведем один из возможных примеров. Рассмотрим равнобедренный треугольник АВС, в котором АВ = ВС = 3, АС = 1 (см. рис. 7). Пусть ВН – его высота, АD и CE – биссектрисы, M – точка пересечения медиан. Тогда BE : EA = BD : DC = AB : AC = 3 : 1 (по свойству биссектрисы треугольника).

Пусть отрезок DE пересекает ВН в точке K, тогда BK : KH = 3 : 1 (по теореме о пропорциональных отрезках). BM : MH = 2 : 1 (по свойству медиан треугольника). Следовательно, точка G лежит вне треугольника DEH, образованного основаниями биссектрис.

5.3. Найдите все трехзначные числа, квадраты которых оканчиваются на 1001.

Первый способ. Пусть = 100а + 10b + c – искомое число. Тогда .

Последняя цифра этого числа зависит только от с2. Так как с2 оканчивается на 1, значит, c = 1 или c = 9. Предпоследняя цифра зависит от выражения 20bc + c2 = . Перебором находим, что окончанию 01 могут удовлетворять только три пары значений (b; c): (5; 1), (0; 1) или (4; 9). Таким образом, квадрат искомого числа имеет вид: или или .

Перебором убеждаемся, что в первом случае ни одно значение а не удовлетворяет условию, во втором случае а = 5, а в третьем – а = 7.

Второй способ. Пусть n – искомое число. Так как n2 оканчивается на 1001, то n2 – 1 = (n – 1)(n + 1) оканчивается на 1000, то есть оно кратно 1000. Поскольку ровно одно из чисел n – 1 или n + 1 может делиться на 5, значит это же число должно быть кратно 125. Оба этих числа – четные, значит, то из них, которое делится на 125, делится и на 250.

Так как искомое число – трехзначное, то остается проверить, на что оканчиваются произведения в семи возможных случаях: 248×250; 250×252; 498×500; 500×502; 748×750; 750×752; 998×1000. На 1000 оканчиваются только два из них:×502 = тогда n – 1 = 500 Û n = 501;×750 = тогда n + 1 = 750 Û n = 749.

Источник

Найдите все натуральные nn такие что n3 1n3 1 является степенью возможно первой простого числа

Первый тур ( 10 минут; каждая задача – 6 баллов ).

Отметим, что условие задачи избыточно, так как OA×OB = OC×OD (степень точки О относительно данной окружности).

1.3. При каких натуральных n число n 2 – 1 является степенью простого числа>?

Ответ : при n = 2 или n = 3.

Во втором случае n – 1 = 1, то есть n = 2.

Второй тур ( 15 минут; каждая задача – 7 баллов ).

Ответ : да, существует.

Таким образом, при α = все члены данной последовательности принимают одно и то же отрицательное значение.

2.2. На каждой грани правильного тетраэдра с ребром 1 во внешнюю сторону построены правильные тетраэдры. Четыре их вершины, не принадлежащие исходному тетраэдру, образовали новый тетраэдр. Найдите его ребра.

Остальные ребра искомого тетраэдра вычисляются точно так же, поэтому имеют ту же длину.

2.3. Может ли объединение двух треугольников оказаться 13-угольником?

Ответ : нет, не может.

Третий тур ( 20 минут; каждая задача – 8 баллов ).

3.3. В однокруговом турнире участвуют 10 шахматистов. Через какое наименьшее количество туров может оказаться так, что единоличный победитель уже выявился досрочно? ( В каждом туре участники разбиваются на пары. Выигрыш – 1 очко; ничья – 0,5 очка; поражение – 0 ).

Ответ : через 7 туров.

После 7 туров вполне могла сложиться ситуация, когда у лидера – 7 очков, а у каждого из остальных участников – меньше, чем 5 очков. Например, это возможно, если лидер свои партии выиграл, а все остальные партии закончились вничью. Тогда, у двух шахматистов, еще не игравших с лидером, – по 3,5 очка, а у других – по 3 очка. Так как до конца турнира осталось 2 тура, то в этом случае победитель уже определен.

Построение примера описано выше.

Четвертый тур ( 25 минут; каждая задача – 9 баллов ).

Сложим эти неравенства почленно и получим требуемое неравенство

4.3. Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?

Ответ : при n = 4 или n = 6.

Из условия задачи следует, что рыцарей – не менее четырех. Заметим, что у рыцаря не может быть более двух друзей, иначе найдутся 4 рыцаря, у которых есть общий враг, но тогда у этого врага, в свою очередь, будет не менее четырех врагов, что противоречит условию. Значит, у каждого рыцаря не более двух друзей и ровно три врага, следовательно, всего рыцарей – не более шести.

Примеры: если рыцарей – 4, то друзей ни кого из них нет и каждый враг каждому, а если рыцарей – 6, то разбиваем рыцарей на две тройки и каждый рыцарь дружит с рыцарями из своей тройки и враждует с рыцарями из другой.

Рассмотрим теперь дополнительный граф с n вершинами (ребра теперь обозначают дружбу. Тогда случай n = 4 реализуется в виде графа без ребер.

Пусть теперь n > 4. Из любой вершины графа выходит n – 4 ребра, а так как отношение дружбы транзитивно, то в графе есть полный подграф из n – 3 вершин. Для остальных вершин графа все вершины этого подграфа являются “врагами”, поэтому n – 3 3, то есть n 6. Таким образом, возможен только случай n = 6 (см. рис. 5).

Пятый тур ( 15 минут; каждая задача – 7 баллов ).

Следовательно, искомый график задается уравнением y = x 2 – 4 x – 1 ⇔ y = ( x – 2 ) 2 – 5.

Источник

Найдите все натуральные nn такие что n3 1n3 1 является степенью возможно первой простого числа

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .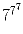

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник