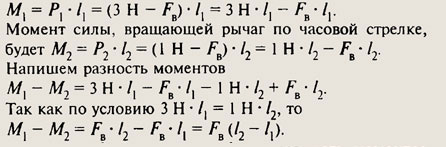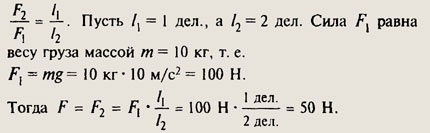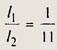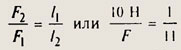на линейку подвесили грузы так что приложенные силы обратно пропорциональны их плечам однако линейка

На линейку подвесили грузы так что приложенные силы обратно пропорциональны их плечам однако линейка

ОТВЕТЫ И РЕШЕНИЯ

Рычаги

Когда мы разламываем спичку, то, скажем, фиксируем один ее конец между пальцами, а на другой конец воздействуем некоторой силой. Спичка ломается в точке опоры под действием момента приложенной силы. Вспомним, что моментом силы называется произведение силы на плечо. А плечом называют кратчайшее расстояние от точки опоры до линии действия силы. Приблизительно можем считать, что в нашей задаче плечо — это длина спички от конца до точки опоры. Считаем спичку однородной, т. е. чтобы разломить ее в разных частях, требуется создать один и тот же момент силы. Так как произведение силы на плечо должно оставаться постоянным, то чем короче спичка (плечо), тем большую силу необходимо приложить, чтобы создать требуемый для перелома момент силы.

Дверь — это физическое тело, имеющее ось вращения. Чтобы заставить дверь вращаться, к ней необходимо приложить силу в определенном месте, которое будет определять момент силы, вращающей дверь. Важно понимать, что вращение любого тела возникает под действием именно момента сил, а не собственно сил. Это действие зависит как от величины силы, так и от ее плеча. (Моментом силы относительно оси вращения или точки опоры называют произведение величины силы на кратчайшее расстояние (плечо) от оси (или точки опоры) до линии, вдоль которой действует сила.) Например, если сила прикладывается к самой оси вращения, то никакого вращения тела вокруг этой оси происходить не будет. Ясно, что, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. При этом с помощью небольшой силы создается значительный вращающий момент. Этот момент необходимо создать не только для того, чтобы преодолеть сопротивление сил трения в петлях двери, но и чтобы преодолеть инерционность, свойственную всем физическим телам.

Замечание. Как известно, мерой инертности (инерционности) тел является масса. Для описания вращения тел вместо массы принято использовать так называемый момент инерции. Он учитывает форму тел. Чтобы раскрутить два тела, имеющие одинаковую массу, но разную форму, до одной и той же угловой скорости вращения, требуется приложить разные моменты силы. Вообще говоря, момент силы — векторная физическая величина, которая кроме абсолютного значения характеризуется еще и направлением действия. В школьном курсе физики момент силы считают для простоты скалярной величиной, а направление действия моментов различают, приписывая разные знаки моментам, вращающим тело по часовой стрелке и против направления ее движения.

Условие равновесия рычага гласит, что рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам. Из рис. 202 видно, что плечо АО меньше плеча ВО. Следовательно, сила, приложенная к точке А, должна быть больше силы, приложенной к точке В. На рисунке же силы изображены одинаковыми.

При подъеме груза на кран действует момент силы тяжести груза, который стремится опрокинуть кран в сторону груза. Величина этого момента равна произведению силы тяжести груза на плечо (расстояние по горизонтали от точки подъема груза до ближайшей точки опоры — колеса). Чем больше вынос стрелы крана (плечо), тем больше получается опрокидывающий момент. Таким образом, масса поднимаемого груза получается ограниченной не столько мощностью лебедки и прочностью тросов, сколько устойчивостью крана во время работы. Можно сказать, что кран представляет собой своеобразный рычаг 1 рода, точкой опоры которого являются ближайшие к грузу колеса, а плечами — стрела и корпус крана. Момент, создаваемый корпусом крана, должен несколько превосходить момент, создаваемый стрелой. Тогда кран будет устойчиво стоять на четырех колесах. Чтобы увеличить массу поднимаемого груза, на кране устанавливают противовес. Он создает момент силы, который уравновешивает в значительной степени опрокидывающий момент стрелы с грузом. Массу противовеса и место его расположения выбирают так, чтобы он не опрокидывал порожний кран. Таким образом установка противовеса позволяет увеличить массу поднимаемого груза.

а) Точка опоры — место подвеса весов. Плечи рычага приблизительно считаем равными половине его длины. Силы направлены вниз:

б) точка опоры — конец стержня, лежащий на столе. Одно плечо равно расстоянию от точки опоры до точки подвеса груза, второе плечо равно длине стержня. Сила со стороны груза действует вниз, а сила со стороны пальца — вверх;

в) точка опоры — конец стержня, упирающийся в крышку стола. Одно плечо равно расстоянию от точки опоры до места обхвата стержня рукой. Второе плечо равно расстоянию от точки опоры до точки подвеса груза. Сила со стороны руки направлена вверх, а сила со стороны груза — вниз;

г) точка опоры — локтевой сустав. Одно плечо — расстояние от сустава до центра ладони, второе плечо — расстояние от сустава до места прикрепления мышцы. Сила со стороны мышцы направлена вверх, а со стороны шара — вниз;

д) ось вращения — ось резьбовой шпильки. Одно плечо равно расстоянию от оси шпильки до места обхвата ключа рукой. Другое плечо примерно равно радиусу шпильки. Сила трения между гайкой и шпилькой направлена в сторону, противоположную направлению вращения гайки (направлению силы со стороны руки);

е) точка опоры — место, где доска опирается о козлы. Левое плечо — расстояние от точки опоры до точки, лежащей между детьми. Правое плечо — расстояние от точке опоры до мальчика. Обе силы направлены вниз;

ж) ось вращения (точка опоры) — ось, за которую ручка крепится к насосу. Левое плечо — расстояние по горизонтали от точки опоры до штока поршня насоса. Правое плечо — расстояние вдоль ручки от точки опоры до места обхвата ручки насоса рукой. Сила со стороны штока направлена вертикально. Сила со стороны руки направлена перпендикулярно ручке. Обе силы направлены либо вверх, либо вниз;

з) точка опоры — ось крепления линейки к штативу. Одно плечо равно 4 делениям, а второе — 6. Сила со стороны грузиков направлена вниз, а со стороны динамометра — вверх.

Ножницы представляют собой как бы два рычага, скрепленных на общей оси вращения. К одному концу этих рычагов прикладывается сила со стороны руки человека, а к другому — сила сопротивления со стороны разрезаемого предмета. Точка приложения силы сопротивления находится в месте соприкосновения лезвий ножниц и перемешается от оси вращения к концам лезвий по мере смыкания концов ножниц. Таким образом, соотношение плеч рычагов меняется в процессе резки. Разрезание бумаги и ткани не требует значительных усилий. Поэтому соотношение плеч (короткие ручки и длинные лезвия) подобрано таким образом, чтобы усилий пальцев рук хватало для удобной работы, а длинные лезвия позволяют за один раз сделать большой непрерывный надрез. Разрезание листового металла требует больших усилий, поэтому соотношение плеч (длинные ручки и короткие лезвия) подобрано так, чтобы получить выигрыш в силе за счет короткого разреза. При этом усилий рук хватает, чтобы преодолеть сопротивление металла.

Как уже говорилось в предыдущей задаче, работу ножниц можно описать, представляя их в виде двух рычагов, скрепленных на общей оси вращения. Ручки ножниц (одно плечо) имеют фиксированную длину. Второе плечо этих рычагов — переменное. Оно равно расстоянию от оси ножниц до точки резания. Именно в этом месте приложена сила сопротивления разрезаемого материала. Во время резания рычаги находятся как бы в равновесии. То есть момент силы давления со стороны руки равен или превосходит момент силы сопротивления материала. По мере резания момент силы сопротивления (она постоянна) увеличивается за счет увеличения плеча (точка резания перемещается от оси ножниц к концам лезвий). Соответственно должен увеличиваться и момент силы давления руки. Но он может увеличиваться только за счет увеличения величины силы (плечо постоянно). Поэтому наименьшую силу нужно прикладывать, когда картон расположен ближе к середине, а не к концам ножниц.

Для того, чтобы затянуть гайку, необходимо создать определенный момент сил. Обычно прикладывают пару сил на противоположных концах гайки. Парой сил называют систему из двух сил, которые численно равны друг другу и направлены вдоль параллельных прямых в противоположные стороны. Момент пары сил F равен М = Fd, где d — плечо пары, кратчайшее расстояние между линиями действия сил. Чем больше плечо d, тем меньшую пару сил F необходимо приложить, чтобы затянуть гайку. Для этой цели на гайке-барашке и делают лопасти. Усилий пальцев при этом хватает, чтобы затянуть гайку, не используя ключи.

Мы знаем, что рычаг находится в равновесии, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки. Момент силы равен произведению величины силы на плечо. На рис. 206, а левое плечо рычага равно 1 делению, правое — 3 делениям. Поэтому мы можем записать равенство 1 • 3 Н = 3 • F. Отсюда сила Г— 1 Н. На рис. 206, б левое плечо равно 2 делениям, правое — 1 делению. Слева подвешен груз массой 5 кг. Он действует на рычаг силой своего веса mg = 5 кг • 10 м/с 5 = 50 Н. Таким образом, из условия равновесия получаем: 50 Н • 2 = F • 1. Отсюда F= 100 Н.

Ответ: а) 1 Н; б) 100 Н.

Судя по рисунку, грузы имеют одинаковый объем. Значит, при погружении в воду на них будут действовать одинаковые выталкивающие силы. В воздухе система грузов находится в равновесии. Левое плечо рычага L₁= 1 дел., правое плечо L₂ = 3 дел.

Условие равновесия: 3 Н • L₁ = 1 Н • L₂.

Момент силы, вращающей рычаг против часовой стрелки, станет равным

Поскольку L₂ больше, чем L₁, то разность моментов больше нуля. Таким образом, момент М₁ больше момента M₂. Равновесие нарушится и груз 3 Н опустится вниз.

Ответ: перетянет груз с надписью 3 Н.

На рис. 208 нанесены разные обозначения: 19,6 Н обозначает величину приложенной силы, а 1 кг обозначает массу подвешенного груза. Груз действует на правое плечо рычага силой своего веса

P=mg=1 кг • 9,8 м/с 5 = 9,8 Н.

Измерив плечи рычага, находим, что правое плечо рычага в два раза больше левого.

Запишем это условие: L_п = 2L_л

Момент силы, вращающей рычаг против часовой стрелки, равен М_п = 19,6 Н • L_л

Момент силы, вращающей рычаг по часовой стрелке, будет М_п = 9,8 Н • L_л = 9,8 Н • 2L_л = 19,6 Н • L_л = M_л. Таким образом, мы получили равенство Мп = Мд, т. е. получили условие равновесия рычага. Значит, система находится в равновесии.

Если взяться за край ручки тисков, то увеличится момент силы затяжки, так как увеличится плечо силы.

В принципе, эта задача решается так же, как задача 736, б. Давайте для разнообразия решим ее, используя не правило моментов, а правило рычага. Оно гласит, что рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:

Пусть длина левого плеча L₁ = 20 см, а длина правого плеча равна L₂. Нам нужно узнать величину L= L₁ + L₂.

Динамометр растянут на 6 делений. Левое плечо рычага равно 6 делениям и к нему подвешен груз весом 2 Н. Правое плечо рычага равно 2 делениям. Пусть со стороны пружины динамометра на рычаг действует сила F. Тогда из условия равновесия по правилу моментов получаем равенство 6 дел. • 2 Н = 2 дел. • F. Таким образом F= 6 Н и цена деления динамометра 6 Н : 6 = 1 Н.

Из рис. 213 видно, что отношение плеч рычага равно

Пусть со стороны динамометра на рычаг действует сила F. На рис. 214, а показан рычаг первого рода. Видно,

что отношение плеч рычага равно

Из условия равновесия отношение приложенных сил будет

Получаем F = 110 Н. Динамометр растянут на 11 делений. Значит, цена деления 110 : 11 = 10 Н. На рис. 214, б представлен рычаг второго рода. Сила в 10 Н вращает его против часовой стрелки. Плечо этой силы равно 12 делениям, а момент — 10 Н • 12 дел. Сила F со стороны динамометра вращает рычаг по часовой стрелке. Ее плечо равно 2-м делениям, а момент составляет F• 2 дел. По условию равновесия 10 Н • 12 дел. — F• 2 дел. Находим F = 60 Н. Динамометр растянут на 6 делений, следовательно, цена деления 60 Н : 6= 10 Н.

Ответ; а) 10 Н; б) 10 Н.

Общий вес грузов составляет 3 Н. Плечо, на которое действует вес грузов, равно 4 делениям. Пусть со стороны динамометра на рычаг действует сила F. Найдем ее, используя правило моментов. Плечо силы F равно 6 делениям. Отсюда 6 дел. • F= 4 дел. • 3 Н. Получаем, что F= 2 Н. По третьему закону Ньютона сила, с которой динамометр действует на рычаг (приложена к рычагу), равна по величине силе, с которой рычаг действует на пружину (приложена к пружине). Таким образом, пружина натянута с силой 2 Н.

Примечание. В этой задаче (и в других подобных с симметричным рычагом) весом рычага можно пренебрегать, а можно и не пренебрегать, так как симметричный рычаг и в отсутствие приложенных сил находится в равновесии. Следовательно, собственные моменты сил тяжести правой и левой его половин равны. При составлении уравнения моментов приложенных к рычагу сил эти собственные моменты сил тяжести войдут в правую и левую половины равенства в качестве дополнительных слагаемых и сократятся.

Источник

Рычаг. Равновесие сил на рычаге

Содержание

С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.

Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.

Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).

В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.

Устройство рычага

Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры.

Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.

В обоих случаях у этого рычага есть неподвижная точка опоры – точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.

Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.

Таким образом, рычаги бывают двух видов (рисунок 3):

Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.

Условие равновесия рычага

Рисунок 4. Рычаг.

Рисунок 5. Схематическое изображение рычага.

Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.

С помощью таких опытов было установлено правило равновесия рычага:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил

Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют – правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.

Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.

Примеры задач

Показать решение и ответ

Решение:

Запишем правило равновесия рычага:

$F_1 = F_2 \cdot \frac = gm \cdot \frac = 9.8 \frac<Н> <кг>\cdot 300 \space кг \cdot \frac<0.6 \space м> <3 \space м>= 2940 \space Н \cdot 0.2 = 588 \space Н$.

СИ:
$0.1 \space кг$
$0.2 \space кг$
$0.5 \space м$
$0.2 \space м$

Показать решение и ответ

$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 \frac<Н> <кг>\cdot (0.1 \space кг + 0.2 \space кг) = 9.8 \frac<Н> <кг>\cdot 0.3 \space кг \approx 3 \space Н$.

Запишем правило равновесия рычага:

Найдем массу груза:

$m_3 = \frac = \frac<1.2 \space Н><9.8 \frac<Н><кг>> \approx 0.1 \space г = 100 \space г$.

Источник

Урок по физике для 7 класса «Рычаг»

1.Обеспечить в ходе урока повторение учащимися понятий «мощность» и «механическая работа»;

2.Обеспечить в ходе урока усвоение учащимися следующих понятий: простые механизмы, рычаг; усвоение правила рычага;

3.Привить умения и навыки в работе с рычагом;

4.Устранить пробелы в знаниях единиц измерения.

1.Содействовать формированию научного мировоззрения учащихся на основе объяснения правила рычага;

2.Содействовать трудовому воспитанию школьников путем показа роли знаний о рычаге в повседневной жизни;

3.Развитие и воспитание у школьников эстетических взглядов.

1.Продолжить формирование общеучебных умений и навыков: планирование ответа, сравнение, обобщение, самоконтроль;

2.Содействовать развитию воли и настойчивости в учении посредством решения проблемных задач, вовлечения учащихся в эксперимент;

3.Развитие эмоций учащихся посредством создания на уроке ситуации занимательности;

4.Выработать умение самостоятельно пополнять свои знания в процессе эксперимента;

Оборудование : раздаточные материалы: «Применение рычага», «Вопросы к кроссворду»; цветной мел; рычаг; грузы массой 100 г; компьютер с диапроектором; линейка; карандаш; монеты; палка; тяжелая сумка; мелодия «Сиртаки»; костюмы царя и Архимеда.

3.Объяснение нового материала

4.Закрепление изученного материала

Садитесь. С какими физическими величинами мы познакомились с вами на прошлом уроке?

Механическая работа и мощность.

Для повторения изученного материала предлагаю вам разгадать кроссворд. На доске нарисована сетка для ответов и написаны вопросы. Также вопросы у вас есть на партах.

Первый вопрос: назовите физическую величину, входящую в формулу для нахождения мощности.

Закончите предложение: «Сила совершает положительную работу, если направление движения тела совпадает с направлением…»

Назовите одну из единиц времени.

Единица мощности в СИ?

Выразите словом 1000000 Вт.

По мере разгадывания кроссворда записываю ответы в нужные клетки.

Скажите, пожалуйста, какое слово мы получили в красных клетках кроссворда?

Это слово получилось не случайно. Тема сегодняшнего урока «рычаг». Откройте свои тетради, запишите сегодняшнее число и тему урока.

Физические возможности человека ограничены, поэтому с древних времен он использовал устройства, которые позволяли преобразовывать его силу, в существенно большую. Такие механические устройства называются простыми механизмами. К ним относятся: наклонная плоскость, с помощью которой тяжелый груз можно поднять вкатывая или втаскивая на нужную высоту; блок, который также облегчает подъем грузов и рычаг.

Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту 147 м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу 2,5 т!

Рассказ дополняю рисунками, спроецированными на экран.

Что же такое рычаг? На демонстрационном столе вы видите лабораторный рычаг. Давайте его поподробней рассмотрим. Из чего он состоит?

Я согласна, это линейка. Но мы с вами учимся владеть физическими терминами. Попробуйте ее назвать с этой точки зрения.

Правильно. А какое это тело?

Молодцы! Что еще мы можем про него сказать? Оно может двигаться? А как?

Это твердое тело и оно способно вращаться.

А как оно вращается?

Вокруг неподвижной оси.

Хорошо! А теперь попытайтесь все вместе собрать и дать определение рычагу.

Рычаг – это твердое тело, способное вращаться вокруг неподвижной опоры.

Давайте запишем это определение к себе в тетради.

Вы видите, что к рычагу подвешены грузы. Они действуют на него с некоторыми силами. Как вы думаете, куда направлены эти силы?

С этими силами связано еще одно понятие, плечо силы. Плечом силы называется расстояние от неподвижной опоры до точки, в которой приложена сила. Обозначается оно маленькой латинской буквой «л». Сколько плечей у нашего рычага?

Мы дали определение рычагу, а теперь давайте попробуем его изобразить схематически. На доске вы видите нарисованную схему рычага с действующими на него силами и их плечами. Зарисуйте ее, пожалуйста к себе в тетради.

Пока ученики зарисовывают, поясняю чертеж и ввожу обозначения сил и их плечей.

Скажите, пожалуйста, находится ли рычаг в равновесии?

А как вы думаете, почему? Ведь с одной стороны на него действуют два груза, а с другой три.

Они висят на разных расстояниях от неподвижной опоры.

Верно, у этих сил разные плечи. Сравните их, пожалуйста.

Большей силе соответствует меньшее плечо, а меньшей силе – большее.

Правильно. Получается, что меньшая сила уравновешивает большую. Рычаг дает выигрыш в силе. Давайте попробуем его найти.

Правильно. Давайте их найдем. Учтем, что масса каждого груза равна 100 г. Чему равна сила тяжести, действующая на один груз?

А в каких единицах измерения вы брали массу груза?

В системе СИ масса измеряется в килограммах. Поэтому массу груза при вычислениях мы брали равной 0,1 кг.

Молодцы! Так чему же равны силы, действующие на рычаг?

Хорошо! Так какой же выигрыш в силе в данном случае дает рычаг?

Выигрыш в силе равен1,5.

А как вы его получили?

Мы большую силу разделили на меньшую.

На доске записываю, что отношение сил равно 1,5.

Как мы уже говорили, эти силы находятся в равновесии из – за разности в их плечах. Давайте найдем плечи сил, действующих на рычаг.

Они равны 30 см и 20 см соответственно.

Подумайте еще раз над ответом и учтите единицы измерения длины в системе СИ.

Плечи сил равны 0,3 м и 0,2 м соответственно.

Правильно. А на сколько одно плечо силы больше другого?

Плечо силы l ₁ больше плеча силы l ₂ в 1,5 раза.

На доске записываю, что отношение плечей сил равно 1,5.

Мы получили в отношениях одно и то же число. Давайте приравняем их. Получили равенство

Из математики вы знаете, что между величинами может существовать прямо пропорциональная и обратно пропорциональная зависимость. Посмотрите на полученное выражение и скажите, как зависят приложенные к рычагу силы от своих плеч?

Приложенные силы обратно пропорциональны своим плечам.

Молодцы! А в каком состоянии при этом находится рычаг?

В состоянии равновесия.

Правильно. Мы получили условие равновесия рычага: рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам.

Это условие называется правилом рычага. Подпишите себе в тетрадях рядом с полученным выражением.

Правило рычага было установлено и использовалось еще в древние времена. Открыл его знаменитый ученый Архимед. Он был величайшим математиком, физиком и инженером древности. В механике им были установлены законы рычага, условия плавания тел и законы сложения параллельных сил.

На экране портрет Архимеда.

Предлагаю вам почувствовать себя в качестве ученых и еще раз проверить правило рычага. Для этого выполните следующее экспериментальное задание.

У каждого на парте найдется линейка, карандаш и несколько монет в кармане. Положите под середину линейки карандаш так, чтобы линейка находилась в равновесии. Не меняя взаимного расположения линейки и карандаша, уравновесьте на полученном рычаге разное количество монет.

После выполнения задания прошу прокомментировать результаты с помощью правила рычага.

Я уравновесил три монеты одной. Там где лежит три монеты, плечо силы меньше, чем там, где лежит одна монета.

Хорошо! Мы еще раз экспериментально подтвердили правило рычага. Давайте повторим его.

Один из учеников рассказывает правило.

Как я уже говорила, рычаг активно использовали в древние времена. В наше время электроники его использование не потеряло актуальности. У вас на партах лежат листочки, в которых описаны случаи применения рычага. Посмотрите, пожалуйста.

С рычагом вы встречаетесь, когда режете ножницами. На правиле рычага основан принцип действия весов. Так же много рычагов находится в теле человека и животных.

Один из примеров применения рычага я предлагаю вам сейчас посмотреть. В этом мне поможет Рома. Я дам ему большую палку и с ее помощью предложу поднять тяжелый груз.

Давайте поможем Роме. Как надо поступить, чтобы держать груз было легче?

Груз надо перевесить ближе к плечу.

Правильно. Стало легче?

Что в данном случае выполняет роль рычага?

А где находится неподвижная опора?

Подвинув груз, какую величину мы изменили, как и для чего?

Мы уменьшили плечо силы, с которой груз действует на палку. Следовательно, сила, которую должен прикладывать Рома, уменьшилась, ему стало легче.

Молодцы! Спасибо, Рома, садись.

Вот такое замечательный рычаг. Спасибо Архимеду, что он открыл его. Но слава к Архимеду пришла не сразу. Ему приходилось доказывать пользу своих открытий.

Начинает звучать музыка. Так, однажды, гуляя по берегу моря с сиракузским царем Гиероном, Архимед предложил использовать рычаг для облегчения труда рабов. Гиерон не поверил ему. Чем закончилась эта история нам сейчас расскажут ребята.

Ученики в костюмах читают по ролям стихотворение под музыку.

Однажды по берегу моря вдвоем

Гулял Архимед с сиракузским царем.

А рядом триеру тащили на мель

И тут Архимед Гиерона спросил:

Ты помнишь мой винт для подъема воды?

В Египте рабам я облегчил труды.

А знаешь, как людям помог бы рычаг

В труде непосильном. К примеру,

Один бы сумел на песчаный причал

Втащить я вот эту триеру.

Стоит Гиерон, потирает висок:

Ты втащишь триеру? Один? На песок?!

Триеру на берег втащу я один.

Триеру с гребцами и грузом.

Вот ты через месяц сюда приходи

И я удивлю Сиракузы.

В назначенный срок собирается люд

На пристани, солнцем согретой.

Глядят на машину, но чуда не ждут:

Не втащит! Да слыхано ль это!

Я вижу веревки и много колес,

И я поражаюсь размеру,

Но даже Геракл, ухватившись за трос,

Не втащит на берег триеру

И тут Архимед повернул колесо –

Триера послушно ползет на песок.

На палубе с ног повалились купцы.

На берег заехать – не шутка!

По воздуху веслами машут гребцы,

Как будто лишились рассудка.

Не верю глазам! Столько силы в плечах?!

Нет, царь! Эту силу умножил рычаг!

Взглянул Архимед: небо, море кругом.

Я землю бы мог повернуть рычагом,

Лишь дайте мне точку опоры.

С этого времени я требую,

Чтобы Архимеду верили во всем,

Что он только не скажет.

Наш урок подходит к концу. Откройте дневники. Запишите домашнее задание: параграф 20, задачи №67, 69, задачи со звездочкой №68, 70.

Давайте подведем итоги сегодняшнего урока.

Какие устройства относятся к простым механизмам?

В чем заключается правило рычага?

Какое из применений рычага вам больше всего запомнилось?

За активную работу на уроке я ставлю оценки…

Урок окончен. Спасибо. До свидания.

Вопросы к кроссворду:

1.Физическая величина, входящая в формулу для нахождения мощности.

2.Закончите предложение: «Сила совершает положительную работу, если направление движения тела совпадает с направлением…»

3.Одна из единиц времени.

4.Единица мощности в СИ.

5.Выразите словом 1 000 000 Вт.

Выигрыш в силе мы имеем при работе с ножницами. Ножницы –это рычаг, ось вращения которого проходит через винт, соединяющий обе половины ножниц.

Действующей силой F ₁ является мускульная сила руки человека, сжимающего ножницы; противодействующей силой F ₂ –сила сопротивления того материала, который режут ножницами.

На принципе рычага основано действие рычажных весов. Учебные весы действуют как равноплечий рычаг.

Использование рычага позволяет поднимать тяжелые предметы. На рисунке изображен рычаг второго рода.

Рычаги встречаются также в разных частях тела животных и человека. Это, например, конечности, челюсти. Много рычагов можно указать в теле насекомых, птиц, в строении растений.

Например, гвоздодер, действуя как рычаг, позволяет выдернуть гвоздь при гораздо меньшем усилии, чем если бы мы попытались сделать это, скажем перочинным ножом. Приложив небольшое усилие к ручке гвоздодера, мы получим на другом его конце большой выигрыш в силе.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник