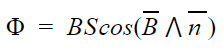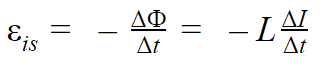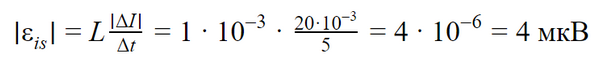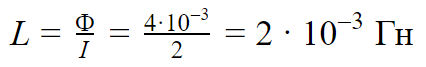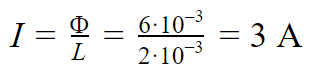можно ли контур содержащий катушку индуктивности резко размыкать почему
Индуктивность контура. Самоиндукция. Токи при размыкании и замыкании цепи



Сцепленный с контуром магнитный поток Ф прямо пропорционален току I в контуре: F = LI, Гн, где коэффициент пропорциональности L называется индуктивностью контура
При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Контур, который содержит индуктивность, нельзя резко размыкать, так как это возникновение значительных ЭДС самоиндукции может привести к пробою изоляции и поломке измерительных приборов.Если в контур сопротивление вводить постепенно, то ЭДС самоиндукции не достигнет больших значений.
Если есть время продиктуй если нет то просто формулу!
Сила тока при размыкании цепи :
Явление самоиндукции
Магнитный поток
Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.
Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.
Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению:
Магнитный поток
Ф — магнитный поток [Вб]
B — магнитная индукция [Тл]
S — площадь пронизываемой поверхности [м 2 ]
n — вектор нормали (перпендикуляр к поверхности) [-]
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Самоиндукция
Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
Формула магнитного потока для самоиндукции
Ф = LI
Ф — собственный магнитный поток [Вб]
L — индуктивность контура [Гн]
I — сила тока в контуре [А]
Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.
Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.
ЭДС самоиндукции
ξis — ЭДС самоиндукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
ΔI/Δt — скорость изменения силы тока в контуре [А/с]
L — индуктивность [Гн]
Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.
Индуктивность
Индуктивность — это способность накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
Можно ли увеличивать индуктивность катушки?
Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.
Как работает катушка
Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.
Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.
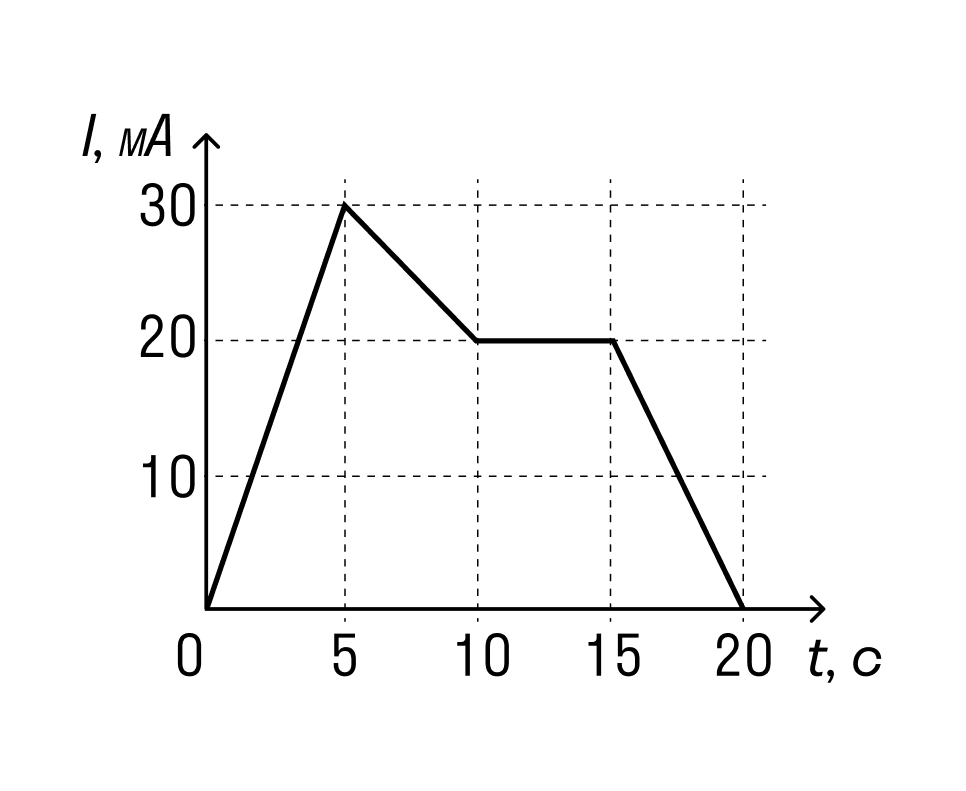
Задачка раз
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.
Решение
За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:
Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.
Задачка два
По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?
Решение
При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.
Отсюда индуктивность катушки равна:
Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:
Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.
Катушка индуктивности
Что такое катушка индуктивности
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
В — магнитное поле, Вб
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Отдалим витки катушки друг от друга
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Самоиндукция. Индуктивность. Токи замыкания и размыкания.
Индуктивность, либо коэффициент самоиндукции (от лат. indactio — наведение, возбуждение) — является параметром электрической цепи, определяющий ЭДС самоиндукции, которая наводитсяв цепи при изменении протекающего по ней тока либо (и) ее деформации.
Термином «индуктивность» обозначают еще и катушку самоиндукции, определяющую индуктивные свойства цепи.
Самоиндукция — образование ЭДС индукции в проводящем контуре при изменении в нем силы тока. Самоиндукция была открыта в 1832 году американским ученым Дж. Генри. Независимо от него в 1835 году это явление открыл М. Фарадей.
ЭДС индукции образуется при изменении магнитного потока. Если это изменение вызывается собственным током, то говорят об ЭДС самоиндукции:

где L — индуктивность контура, либо его коэффициент самоиндукции.
Индуктивность — является физической величиной, численно равной ЭДС самоиндукции, которая возникает в контуре с изменением силы тока на 1 А за 1 секунду.
Индуктивность, как и электроемкость, зависима от геометрии проводника — его размеров и формы, но не зависима от силы тока в проводнике. Таким образом, индуктивность прямого провода намного меньше индуктивности того же провода, свернутого в спираль.
Расчеты показывают, что индуктивность описанного выше соленоида в воздухе вычисляют по формуле:

где μ0— магнитная постоянная, N — количество витков соленоида, l — длина соленоида, S — площадь поперечного сечения.
Также, индуктивность зависит от магнитных свойств среды, в которой находится проводник, а именно от его магнитной проницаемости, определяющаяся при помощи формулы:

где L0 — индуктивность контура в вакууме, L — индуктивность контура в однородном веществе, которое заполняет магнитное поле.
Токи замыкания и размыкания.
При каждом включении и выключении тока в цепи наблюдаются так называемые экстратоки самоиндукции (экстратоки замыкания и размыкания), которые возникают в цепи из-за явления самоиндукции и которые препятствуют, согласно правилу Ленца, нарастанию или убыванию тока в цепи.
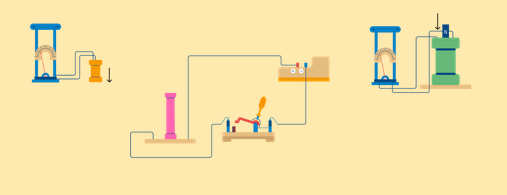
На рисунке выше показана схема соединения 2х одинаковых ламп. Одна из них подключена к источнику через резистор R, а другая — последовательно соединена с катушкой L с железным сердечником. При замыкании цепи первая лампа вспыхивает почти мгновенно, а вторая — с существенным опозданием. Это вызвано тем, что ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения.
При размыкании ключа в катушке L образуется ЭДС самоиндукции, которая поддерживает первоначальный ток.
В итоге в момент размыкания через гальванометр течет ток (светлая стрелка), который направлен против начального тока до размыкания (черная стрелка). При этом ЭДС самоиндукции может быть намного больше ЭДС батареи элементов, что будет проявляться в том, что экстраток размыкания будет сильно превышать стационарный ток при замкнутом ключе.
Индуктивность характеризует инерционность цепи по отношению к изменению в ней тока, и ее можно рассматривать как электродинамический аналог массы тела в механике, являющейся мерой инертности тела. При этом ток I играет роль скорости тела.