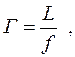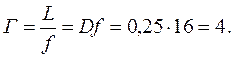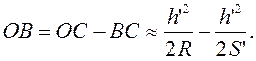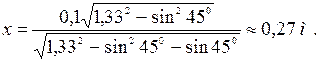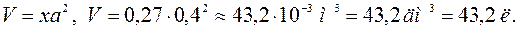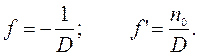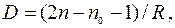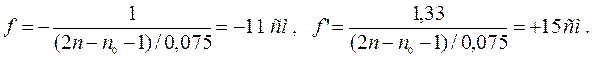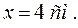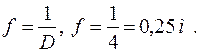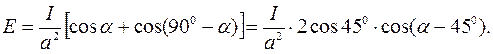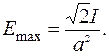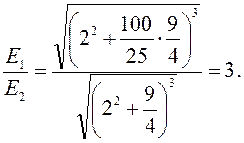кубический сосуд с непрозрачными стенками расположен так что глаз наблюдателя не видит его дна

Кубический сосуд с непрозрачными стенками расположен так что глаз наблюдателя не видит его дна

Тема. Решение задач по теме «Законы отражения и преломления света. Полное внутреннее отражение».

В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности.

Прежде чем приступить к выполнению задания, необходимо повторить основные законы геометрической оптики и определения: луч падающий, отраженный, преломленный, углы падения, отражения, преломления, абсолютный и относительный показатели преломления, явление полного внутреннего отражения.

Получите основные законы геометрической оптики (законы преломления, отражения), применяя принцип Гюйгенса-Френеля для волн на границе двух сред.

Обратите внимание, что законы геометрической оптики и волновой оптики проявляются в физике при определенных физических условиях и имеют свои границы применимости.

Примеры решения расчетных задач

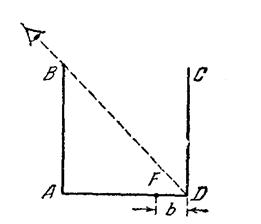
Задача 1. Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит стенку CD. До какой высоты h надо заполнить сосуд водой (n = 4/3), чтобы наблюдатель смог увидеть предмет F, находящийся на расстоянии b = 10 см от точки D?

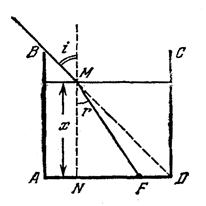
Так как, согласно условию задачи, глаз не видит дна сосуда, а сосуд имеет форму куба, угол падения луча зрения на поверхность жидкости равен α = 45° (рис. 2).

Из прямоугольного треугольника NKF видно, что .
Отсюда . (1)

Согласно закону преломления .
Тогда

; . (2)
После подстановки (2) в (1) получим:

Ответ:

Задача 2. Световой луч распространяется в стекле с показателем преломления n = 1,5. На его пути встречается щель, заполненная воздухом. Грани щели плоские и параллельные, расстояние между гранями равно d = 3 см, угол падения луча на грань α = 30°. На какое расстояние сместится световой луч, вышедший из щели, относительно продолжения падающего луча?

см.

Ответ: .

Задача 3. На дне стеклянной ванны лежит зеркало, поверх которого налит слой воды высотой d = 20 см. В воздухе на высоте l = 30 см над поверхностью воды висит лампа. На каком расстоянии от поверхности воды смотрящий в воду наблюдатель увидит изображение лампы в зеркале? Показатель преломления воды n = 1,33.

Для построения изображения S´ выберем два луча (рис. 4). Луч 1, направленный из точки S по нормали к поверхности воды, не преломляется. Луч 2, направленный под небольшим углом i к нормали, в точке К преломляется. Обозначим угол преломления через r. Преломленный луч падает на зеркало З в точку D под углом i, отражается от зеркала под углом r и на границе вода-воздух в точке С выходит под углом i к нормали. На пересечении луча 1 и продолжения луча 2 в точке S´ находится мнимое изображение точки S.

Из прямоугольного треугольника S´ОС выразим h:

.
Из прямоугольного треугольника SOK получим OK = l · tg i. Из треугольника KCD получим KC = 2d · tg r. Тогда

.
Так как для малых углов tg i ≈ sin i, то , тогда

Ответ:.

Задача 4. На нижней стороне плоскопараллельной стеклянной пластинки нанесена чернилами точка, которую наблюдатель видит на расстоянии h = 5 см от верхней поверхности. Определите толщину d пластинки, если луч зрения перпендикулярен к поверхности пластинки, показатель преломления стекла n = 1,6. Считать для малых углов
sin α ≈ tg α ≈α.

Чернильное пятно, находящееся в точке А на нижней стороне стеклянной пластинки, рассматривается сверху и, как видно из рис. 5, кажется находящимся в точке A´. Поясним это. Направим в точку А два луча: луч 1 идет по нормали, не преломляясь. Луч 2, направленный под небольшим углом α, преломляется. Обозначим угол преломления через i. Преломленный луч падает в точку В под углом преломления i и выходит из пластинки под углом α. Чернильное пятно кажется находящимся на пересечении луча 1 и продолжения луча 2, проведенного из точки В в точку A´.

Из прямоугольного треугольника АВС видно, что . Из прямоугольного треугольника A´ВС: BC = h · tg α. После подстановки ВС получим для d:

Задача 5. В воду опущен прямоугольный стеклянный клин с показателем преломления стекла n = 1,5. При каком минимальном значении угла α (рис. 6) луч света, падающий нормально на грань АВ, достигнет грани АЕ? Под каким углом β он выйдет из призмы?

Чтобы луч света полностью вышел из призмы, необходимо, чтобы он падал на грань ВЕ в точке падения С под углом α_пред, который по построению равен искомому углу призмы α (рис. 7). В соответствии с законом преломления
Отсюда sin α_пред = 0,8888, α_пред = α = 62°30´.

откуда , β ≈ 40°19´.

Ответ: α = 62°30´; β = 40°19´.

Задачи для самостоятельной работы

Источник

Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя

Условие задачи:

Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит заднюю вертикальную стенку. Сколько воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет, находящийся на расстоянии 10 см от задней стенки сосуда на его дне? Ребро сосуда 40 см.

Задача №10.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Теперь займемся правым рисунком. Из равенства (1) следует, что угол \(\alpha\) равен 45°, и это очень важный вывод. Значит в прямоугольном треугольнике, образованном лучом, стенкой сосуда и поверхностью воды, оба катета равны \(\left( \right)\) (смотрите рисунок справа).

Для ситуации на рисунке справа запишем закон преломления света (также известен как закон преломления Снеллиуса):

Здесь \(\alpha\) и \(\beta\) – угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) – показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Попытаемся найти синус угла \(\beta\), для чего найдем противолежащий катет \(x\) в соответствующем прямоугольном треугольнике.

\[x = a – l – \left( \right)\]

Сделаем важную оговорку: так как \(x\) не может быть меньше нуля, то \( > \), это пригодится нам в дальнейшем решении.

Тогда синус угла \(\beta\) найдем по формуле (гипотенузу в том же прямоугольном треугольнике найдем по теореме Пифагора):

Подставим в уравнение (2) выражения (1) и (3):

Как Вы должны понимать, физика в этой задаче закончилась, осталась только математика – нужно решить данное уравнение. Перепишем его в следующем виде:

Возведем в квадрат обе части этого уравнения:

Раскроем скобки в обеих частях уравнения:

\[n_1^2 – 2n_1^2hl + n_1^2 + n_1^2 = 2n_2^2 – 4n_2^2hl + 2n_2^2\]

Перенесем все в правую часть и сгруппируем:

Решим данное квадратное уравнение относительно \(\frac\), для чего перейдем к нахождению дискриминанта:

\[D = 16n_2^4 – 16n_1^2n_2^2 + 4n_1^4 – 16n_2^4 + 8n_1^2n_2^2 + 16n_1^2n_2^2 – 8n_1^4\]

\[D = 8n_1^2n_2^2 – 4n_1^4\]

Учитывая численные значения показателей преломления, нетрудно сделать вывод, что дискриминант – положительный. Тогда корни уравнения следующие:

Посчитаем численное значение корней:

Как Вы видите, второй корень не удовлетворяют условию \( > \). Значит уровень воды \(h\) равен:

Искомый объем воды легко найти по формуле:

Ответ: 43 л.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник

Примеры решения задач. Какое увеличение дает лупа, оптическая сила которой 16Дптр?

Задача 1.

Какое увеличение дает лупа, оптическая сила которой 16Дптр? Построить изображение предмета в лупе.

Решение.

Увеличение, даваемое лупой, рассчитывают по формуле:

где 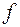– фокусное расстояние лупы; – расстояние наилучшего зрения (равно 25 см для нормального глаза).

Для того чтобы рассмотреть предмет через лупу, его располагают между лупой и ее фокусом (Рис. 1).

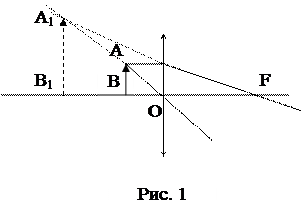Для построения изображения точки А этого предмета используем два луча, исходящих из нее: один, параллельный главной оптической оси, после преломления проходит через фокус; другой, проходящий через главный оптический центр линзы, не изменит своего направления. Изображение А₁ точки А получается в точке пересечения продолжений преломленных лучей. Аналогично получаем изображение В₁ точки В. Следовательно, изображение А₁В₁ предмета АВ будет мнимое, увеличенное и прямое.

Ответ: изображение предмета АВ будет мнимое, увеличенное в 4 раза и прямое.

Задача 2.

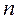
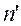
Вывести с помощью принципа Ферма формулу преломления параксиальных лучей на сферической поверхности радиуса R, разделяющей среды с показателями преломления и .

Решение.

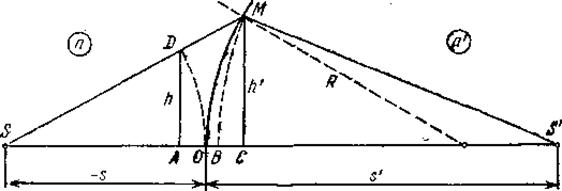
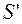
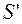
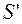
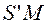
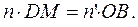
Параксиальные (приосевые) лучи – это лучи, образующие с оптической осью малые углы. Пусть S – точечный источник света и – его изображение (Рис. 2). По принципу Ферма оптические длины всех лучей, вышедших из S и собравшихся в , одинаковы. Проведем окружности из центров S и радиусами SO и . Тогда оптические пути (DM) и (OB) должны быть равны:

(1)

Но для параксиальных лучей:

,

и .

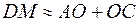
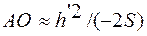
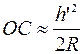
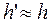
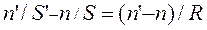
Подставив эти выражения в (1) и имея в виду, что , получим:

.

Ответ: .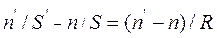

Задача 3.

Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит стенку CD (Рис. 3).

Какое количество воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет F, находящийся на расстоянии b=10 см от угла D? Ребро сосуда а=40 см.

Решение.

Минимальное количество воды, определяемое уровнем x (Рис. 3а), можно найти из треугольника MNF, NF=x-b=x·tg r.

Дано:	СИ:	Рис. 3а
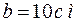=	0,1 м
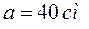=	0,4 м
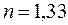Найти: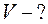

Из закона преломления: sin r= sin i/n.

.

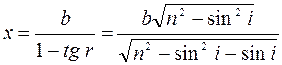
Подставив значения и произведя вычисления, получим:

Необходимый объем воды:

Ответ: 43,2 л.

Задача 4.

Найти положение главных плоскостей, фокусов и узловых точек двояковыпуклой тонкой симметричной стеклянной линзы с радиусом кривизны поверхностей R=7,50 см, если с одной стороны ее находится воздух, а с другой – вода.

Решение.

Главные плоскости совпадают с центром линзы. Фокусные расстояния в воздухе и воде:

Оптическая сила линзы равна:

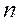
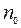
где и — показатели преломления стекла и воды.

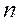
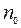
Из справочных таблиц для стекла =1,5 и для воды =1,33. Согласно условию R=7,50 см или R=0,075 м.

Произведя вычисления, получим:

Узловые точки совпадают и расположены в воде на расстоянии:

Задача 5.

Телеобъектив состоит из двух тонких линз – передней собирающей и задней рассеивающей с оптическими силами D₁=+ 10 Дптр и D₂=-10 Дптр. Найти фокусное расстояние и положение главных плоскостей этой системы, если расстояние между линзами d=4,0 см.

Решение.

Оптическая сила системы:

Подставляя числовые значения, получаем:

D=+10 – 10 – 0,04·10·(-10) = +4 (-10) = +4 Дптр.

Фокусное расстояние равно:

Определим расстояния, на которых расположены обе главные плоскости от линз.

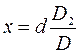
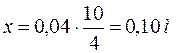
Передняя главная плоскость находится перед собирающей линзой на расстоянии: , вычисляя, получаем: .

Задняя главная плоскость расположена на расстоянии 0,10 м от рассеивающей линзы:

.

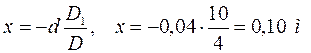
Ответ: f=0,25 м; передняя главная плоскость находится перед собирающей линзой на расстоянии 0,10 м; задняя главная плоскость – на расстоянии 0,10 м от рассеивающей линзы.

Задача 6.

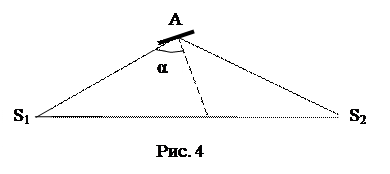
В вершинах равнобедренного треугольника расположены источники света S₁ и S₂ равной силы (Рис. 4). Как следует расположить маленькую пластинку А, чтобы освещенность ее была максимальной? Стороны треугольника AS₁=AS₂=а.

Решение.

Если нормаль к пластинке составляет угол α с направлением AS₁, то освещенность пластинки:

Ответ:

Задача 7.

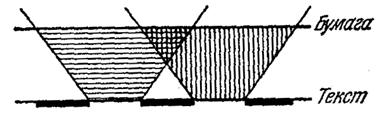
Почему сквозь папиросную бумагу можно прочесть текст только в том случае, если бумагу непосредственно наложить на страницу книги?

Решение.

Папиросная бумага рассеивает во все стороны падающие на нее световые лучи. Если бумага находится на некотором расстоянии от текста книги, то расходящиеся пучки света, отраженные от белых участков страницы (между буквами), перекрываются на стороне папиросной бумаги, обращенной к тексту (Рис. 5).

В результате бумага окажется освещенной приблизительно равномерно, и вследствие рассеяния ею света прочитать текст будет нельзя. Если бумага непосредственно наложена на текст, то освещенность прилегающей к тексту стороны бумаги не будет равномерной. Соответственно интенсивность рассеянного света будет различной в различных участках листа бумаги. Это и позволяет прочитать текст.

Задача 8.

На высоте Н₁=2 м над серединой круглого стола (Рис. 6) диаметром D=3 м висит лампа в I₁=100 Кд. Ее заменили лампой в I₂=25 Кд, изменив расстояние до стола так, что освещенность середины стола осталась прежней. Как изменится освещенность края стола?

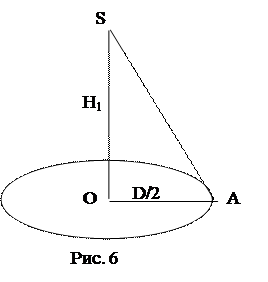
Дано:	Решение. Сделаем чертеж.
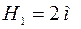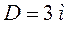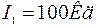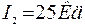Найти: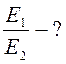

Освещенность середины стола:

,

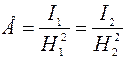
где 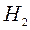— высота второй лампы над столом.

Освещенность края стола в первом случае равна:

,

.

.

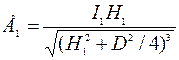
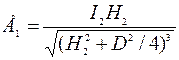
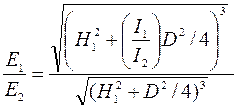
Подставив значения, получим:

Освещенность края стола уменьшится в 3 раза.

Ответ: освещенность края стола уменьшится в 3 раза.

Домашнее задание:

[Л-3] – 15.14, 15.35, 15.38, 15.41, 15.59, 15.62, 15.63, 15.66, 15.67, 15.68;

[Л-4] – 4.3, 4.6, 4.8, 4.9, 4.10, 4.14, 4.14, 4.24, 4.26, 4.27;

[Л-5] – 5.11, 5.15, 5.16, 5.18, 5.29, 5.30, 5.35.

Вопросы для самопроверки

1. Что называют фотометрией?

2. Как построить изображение предмета, если он значительно больше линзы?

3. Почему в тонкостенном стакане с водой ложечка кажется увеличенной?

4. При каком условии непрозрачный предмет дает тень без полутени?

5. Как должна быть расположена лампочка в карманном фонаре относительно главных фокусов собирающей линзы и вогнутого зеркала?

6. Как надо расположить собирающую и рассеивающую линзы, чтобы параллельные лучи, пройдя через линзы, остались параллельными? При всяких ли линзах возможно решение этой задачи?

7. Почему в фотометрии вводятся двойные величины (энергетические и визуальные)?

8. Что называется энергетическим световым потоком?

9. Связь между светимостью и яркостью.

10. Определение единицы светового потока – люмена.

11. Определение единицы освещенности – люкса.

12. Зависит ли яркость раскаленного шара от расстояния до него?

13. Часто под действием солнечных лучей снег на крыше тает, а на почве нет. Почему?

14. В какое время дня освещенность земной поверхности большая?

Источник