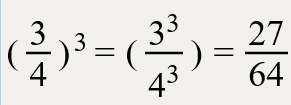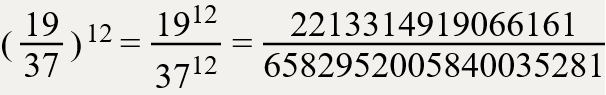что такое 2 3 части в математике
2/3 части это сколько? Две третьи, это сколько?
2/3 части это сколько? Две третьи, это сколько?
2/3 части какого-либо значения величины означает, что это значение нужно разделить на 3 и умножить на 2. Например, две третьи от числа 24 будет равна 16, 24:3 = 8, 8*2 = 16.
Так же находим 2/3 любого другого числа или величины. Например, 2/3 площади квартиры, если площадь равна 40 кв. метрам, то 2/3 от этой площади будет равна 40 кв. метрам.
Не любое число делится на 3, поэтому часто получаются дробные значения или бесконечные десятичные дроби при нахождение 2/3 части. Например, две трети 100, это примерно 66,7.
чтобы возвести дробь в степень надо возвести в степень и числитель и знаменатель
Результатом возведения дроби в степень будет новая дробь у которой числитель равен числителю этой дроби в возведенному в степень, а знаменателем будет знаменатель этой дроби в возведенный в степень.
(¾)³=3³/4³=27/64
Так и с дробями. Дроби с разными знаменателями сродни измерению в разных системах. Сами по себе они могут так жить преспокойно, со своими уникальными знаменателями, пока не придёт время их сравнить, или сложить. Вот тут то и нужно их привести к чему-то одному, ‘компромиссному’. При переводе к единому знаменателю числители у этих дробей и выйдут тогда из ‘сумерка’, показав свой истинный вес.
Также добавлю, что для четных чисел ответ на такое же задание будет 0, так как там присутствует как минимум одно число заканчивающееся на 0, например 10.
Здесь можно только сократить, по формуле разности квадратов. Нужно представить в виде c=(√с)^2, и 3=(√3)^2. Тогда числитель (с-3) можно представить в виде ((√с)^2-(√3)^2) и разложить его на множители в виде (√с-√3)*(√с+√3). Теперь в числителе есть одинаковый со знаменателем множитель, и на него можно сократить. Остаётся (√с-√3).
Ну если это уравнение с параметром, то нужно еще доп. сведение, если трансцендентное уравнение, то решение проблематичное, ибо надо заниматься подстановкой.
Однако кое-что все же ясно.
X надо найти, а вот «a» яко бы известно.
1) Нарисовать график, допустим y=3,335;
P.P.S. Для решения используем калькулятор или ПО Excel, что бы облегчить ПодбоР! корня. Также используем метод последовательных приближений с заданным интервалом вдоль явного решение, которое соответственно равно g(x)=y=3,335.
Т.к. f(x)=x/a начнем подбор x и «а» одновременно.
Продолжая последующие итерации, постоянно увеличивая приближения от десятых до сотых и тысячных, находим значение константы «a» и корня x.
P.P.P.S Если же это уравнение с параметром или что более верно уравнение с буквенной частью, то все еще проще:
Напоследок, безусловно для любого решения «a» не равно нулю, в математике это важно, но все же не считаю я нужным это указать, т.к. мы явно установили вид кривой и явно указали 1 точку пересечения, если б деление было бы на ноль возможно, то первые два утверждения были бы автоматически не верны.
Что такое 2 3 части в математике
В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.
Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

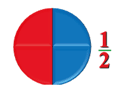
На доли можно разделить окружность:
Доля – это каждая из равных частей целого.
Название доли зависит от того, на сколько частей разделили целое.
Половина
Например, яблоко разделили на две части, получилась половина яблока.
Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.
Прочитать такую долю можно как ОДНА ВТОРАЯ.
Треть
Если целое разделили на три части, то получили ТРЕТЬ, третью часть.
Прочитать такую долю можно как ОДНА ТРЕТЬЯ.
Четверть
Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.
Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.
Запись и чтение долей



Сравнение долей
Для примера сравним две доли: одну шестую и одну третью.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.
Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.
Сравним ещё две доли: одну восьмую и одну четвёртую.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.
Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.
Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.
Поделись с друзьями в социальных сетях:
Задачи на части
Рассмотрим задачи, для решения которых некоторую величину можно принять за одну или несколько частей. При решении таких задач бывает полезно делать рисунки, облегчающие решение.
Задача 1. В двух коробках лежит 120 дисков — в первой коробке в 3 раза больше дисков, чем во второй. Сколько дисков лежит в каждой коробке?
Решение: Представим содержимое коробок в виде частей. Если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке — 3 такие части. Сделаем схематический рисунок:
1) Сколько частей составляют 120 дисков?
2) Сколько дисков приходится на 1 часть?
3) Сколько дисков находится в первой коробке?
Ответ: 90 — в первой коробке, 30 — во второй.
Задача 2. Некто заплатил за книгу на 120 рублей больше, чем за тетрадь. Известно, что книга дороже тетради в 4 раза. Сколько стоит книга?
Решение: Представим стоимость в виде частей. Если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. Сделаем схематический рисунок:
2) 120 : 3 = 40 (рублей) — приходится на 1 часть.
3) 40 · 4 = 160 (рублей) — стоит книга.
Ответ: Книга стоит 160 рублей.
Задача 3. В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. Сколько карандашей в каждой коробке?
Решение: Сделаем схематический рисунок:
1) Если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:
2) Найдём число карандашей в каждой из коробок:
3) Теперь вернём 6 карандашей в первую коробку:
Ответ: В первой коробке 18 карандашей, во второй — 12.
Математика. 3 класс
Конспект урока
Математика, 3 класс
Урок №32. Доли. Образование и сравнение долей
Перечень вопросов, рассматриваемых в теме:
— как записывать, сравнивать доли?
— что значит разделить на равные части (доли) предметы, геометрические фигуры?
Доля – каждая из равных частей единицы.
Деление – действие, обратное умножению.
Делимое – число, которое делят.
Делитель – число, на которое делят.
Частное – результат деления.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, с. 92-93.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016, с. 44-47.
Теоретический материал для самостоятельного изучения
Людям часто приходится делить целое на доли. Самая известная доля — это, конечно, половина. Слова с приставкой «пол» можно услышать, пожалуй, каждый день: полчаса, полкилограмма, полбулки.
Но есть и другие употребительные доли. Например, четверть, десятая, сотая. Когда образуются доли? Тогда, когда один предмет (буханка хлеба, лист бумаги) или единица измерения (час, килограмм) делятся на равные части. Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на две части название доли «половина», на три — «треть», на четыре — «четверть». А если на пять, на шесть, семь частей, то пользуются словами «пятая, шестая, седьмая» и т. д. Четверти по-другому называют четвёртыми, трети – третьими, а половины – вторыми долями.
Для записи любой доли используют горизонтальную черточку. Ее называют дробной чертой. Над ней ставится единица, а под чертой пишется число равных частей, на которые единица делится.
Современное обозначение дробей берет своё начало в Древней Индии; его стали использовать и арабы, а от них в ХII – XIV веках было заимствовано европейцами.
Первым европейским ученым, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фибоначчи (Леонардо Пизанский). В 1202 году он ввёл слово «дробь». Названия «числитель» и «знаменатель» ввёл в ХIII веке Максим Плануд – греческий монах, ученый – математик.
Каждому из вас приходилось делить апельсин. Неразделенный апельсин считается целое, а его части – доли.
В апельсине восемь долек. Мы разделим их пополам. Получились две части или в математике говорят одна вторая и записывается так: 
Число под чертой указывает, на сколько частей разделили, а число, над чертой – сколько таких частей взяли.
Познакомимся с различными записями долей.
На первом рисунке закрашена одна вторая.
На втором рисунке две третьих.
На третьем рисунке закрашено три четвертых.
На четвёртом рисунке закрашено четыре пятых рисунке.
На пятом рисунке закрашена одна шестая.
Доли можно сравнивать. На рисунке один и тот же прямоугольник разделён на равные части. Сравним их.
Наименьшей частью будет одна шестая, а наибольшая одна вторая.
Сравним другие доли. Одна третья меньше одной второй. Одна четвертая больше одной шестой.
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как \(\mathbf\) или же через дробную черту: \(\mathbf<\frac>\)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в \(\mathbf<1\frac<1><4>>\) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в \(\mathbf<\frac<2><3>>\) раза.
Мы можем сформулировать вывод и так: 16 составляет \(\mathbf<\frac<2><3>>\) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно \(\mathbf<\frac<2><5>>\), найдем отношение b к a
Для этого надо найти обратное число к \(\mathbf<\frac<2><5>>\)
Значит, отношение b к a равняется \(\mathbf<2\frac<1><2>>\)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно \(\mathbf<\frac<1><3>>\)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно \(\mathbf<\frac<1><3>>\)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf<\frac<3><8>>\)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна \(\mathbf<2\frac<1><2>>\)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили \(\mathbf<2\frac<1><2>>\), равняется \(\mathbf<\frac<1><4>>\)
Пример 2
Отношение первого числа ко второму равно \(\mathbf<1\frac<1><5>>\), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к \(\mathbf<1\frac<1><5>>\)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно \(\mathbf<1\frac<1><2>>\)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет \(\mathbf<\frac<3><5>>\) от длины всей улицы.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации