что такое 1 радиан в остойчивости
Диаграмма динамической остойчивости

Судно при этом получает динамический угол крена, хотя и кратковременный, но значительно превышающий крен, который мог бы возникнуть при статическом действии этого же момента.
Представим, что к судну, находящемуся в нормальном (прямом) положении внезапно приложен кренящий момент Мкр, под действием которого судно начнет крениться с постоянно нарастающей скоростью (с ускорением), т. к. в начальный период восстанавливающий момент Мв будет нарастать значительно медленнее Мкр.
После достижения судном угла статического равновесия θст, т. е. когда Мкр = Мв, угловая скорость максимальна. Судно по инерции продолжает крениться, но уже с убывающей угловой скоростью (замедлением). Объясняется это тем, что Мв становится больше, чем Мкр.
В какой-то момент угловая скорость становится равной 0, накренение судна прекращается (судно «замрет» в нижней точке крена) и угол крена достигает своего максимума. Этот угол называется углом динамического крена θдин. Затем судно начнет возвращаться в первоначальное положение.
Динамической остойчивостью называют способность судна выдерживать динамическое воздействие кренящего момента.
Относительной мерой динамической остойчивости является плечо динамической остойчивости lдин.
Кривую, выражающую зависимость работы восстанавливающего момента или плеча динамической остойчивости от угла крена, называют диаграммой динамической остойчивости (ДДО).
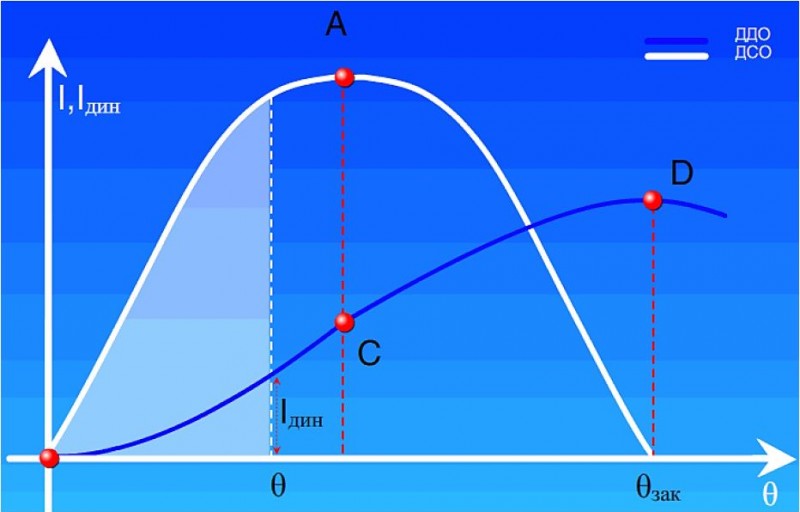
Графическое изображение диаграммы динамической остойчивости по отношению к диаграмме статической остойчивости дано на рис. 9.5., из которого видно, что:
точки пересечения диаграммы статической остойчивости с осью абсцисс отвечают точкам О и D экстремума диаграммы динамической остойчивости;
точка А максимума диаграммы статической остойчивости соответствует точке перегиба С диаграммы динамической остойчивости;
любая ордината диаграммы динамической остойчивости, отвечающая некоторому углу крена θ, представляет в масштабе соответствующую этому углу крена площадь диаграммы статической остойчивости (заштрихована на рисунке).
Диаграммы статической и динамической остойчивости
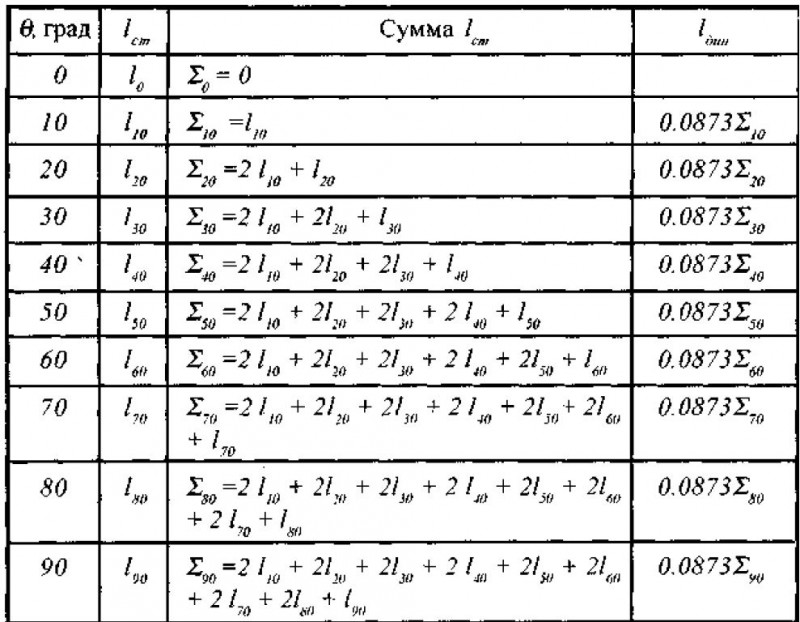
Обычно в судовых условиях строят диаграмму динамической остойчивости по известной диаграмме статической остойчивости, схема вычислений плеч динамической остойчивости приведена в табл:
Плечи динамической остойчивости
Диаграмма динамической остойчивости судна
Точка В практического значения не имеет.
Если построенный таким образом график произведения lкр*θ вообще не пересекает диаграмму динамической остойчивости, то это означает, что судно опрокидывается.
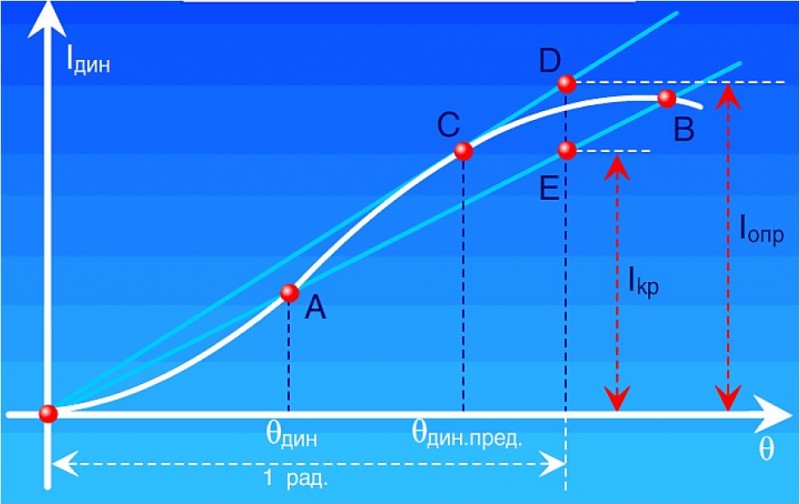
Для нахождения опрокидывающего момента, который еще может выдержать судно не опрокидываясь, следует провести из начала координат касательную к диаграмме динамической остойчивости до пересечения ее в точке D с вертикалью, соответствующей крену в 1 радиан.
Отрезок этой вертикали от оси абсцисс до пересечения ее с касательной дает плечо опрокидывающего момента lопр, а сам момент определится умножением плеча lопр на силу веса судна Р. Точка касания С определит предельный угол динамического крена θдин.преп.
Динамическая остойчивость
Общие положения
Динамической остойчивостью называется способность судна противостоять, не опрокидываясь, динамическому воздействию кренящих моментов.
Динамический кренящий момент возникает от воздействия на судно шквалистого ветра, ударов волн, рывка или толчка буксирного судна, столкновения с другим судно или плавучим объектом, а также льдом.
Предположим, что на судно, внезапно подействовал динамический кренящий момент. Как только, судно накренится на некоторый малый угол, возникнет восстанавливающий момент, который будет стремиться вернуть судно в прямое положение. Поскольку приложенный динамический кренящий момент уже имеет определенное значение, а восстанавливающий момент возрастает постепенно, по мере увеличения плеча восстанавливающего момента, то судно будет продолжать крениться с возрастающей угловой скоростью. При накренении на некоторый угол, восстанавливающий момент сравняется по величине с кренящим моментом, но так как судно имеет некоторую угловую скорость, то оно будет продолжать крениться. По инерции судно кренится далее, но уже с уменьшающейся угловой скоростью, так как постепенно увеличивающийся восстанавливающий момент становится больше кренящего. При достижении некоторого угла динамического крена, когда угловая скорость наклонения станет равной нулю, дальнейшее нарастание крена прекратится и под воздействием восстанавливающего момента судно начнет возвращаться к положению равновесия. Около положения равновесия судно будет совершать колебательные движения, пока они не затухнут под влиянием сопротивления воды и воздуха и судно не остановится при некотором угле равновесия.
Динамическая остойчивость определяется количеством работы восстанавливающего момента при наклонении судна до заданного угла.
Если восстанавливающий момент представить, как
то динамическая остойчивость при любом угле крена может быть вычислена по формуле:
Δ — Водоизмещение судна. 
Плечо динамической остойчивости — это изменение вертикального расстояния между центром тяжести и центром величины при динамическом наклонении судна.
Геометрический смысл возникновения плеча динамической остойчивости показан на рисунке 1. На нем:
Рисунок 1. Пример возникновения плеча динамической остойчивости.
Графически зависимость работы восстанавливающего момента или плеча динамической остойчивости от угла крена изображают в виде диаграммы динамической остойчивости.
Расчет плеч динамической остойчивости
В судовых условиях плечи динамической остойчивости, с приемлемой для практических целей точностью, рассчитывают по известным значениям плеч статической остойчивости для соответствующего угла крена. Для удобства вычислений заполняют таблицу. Пример таблицы приведен ниже.
Таблица для расчета плеч динамической остойчивости:
Пример: Вычисление плеч динамической остойчивости:
В приведенной в примере таблице, интегральная сумма ∑ вычисляется следующим образом:
Для угла крена 10° интегральная сумма равна: 0 + 0 + 0,19 = 0,19
Для угла крена 20° интегральная сумма равна: 0,19 + 0,19 + 0,32 = 0,70
Для угла крена 30° интегральная сумма равна: 0,70 + 0,32 +0,53 = 1,55
Для угла крена 40° интегральная сумма равна: 1,55 + 0,53 + 0,58 = 2,66
Для угла крена 50° интегральная сумма равна: 2,66 + 0,58 + 0,39 = 3,63
Для угла крена 60° интегральная сумма равна: 3,63 + 0,39 + 0,24 = 4,26
Для угла крена 70° интегральная сумма равна: 4,26 + 0,24 + 0,14 = 4,64
Для угла крена 80° интегральная сумма равна: 4,64 + 0,14 + (-0,08) = 4,70
По рассчитанным в таблице значениям плеч динамической остойчивости строят диаграмму динамической остойчивости. Пример ДДО приведен на рисунке 2.
Рисунок 2. Пример диаграммы динамической остойчивости.
Диаграмма статической остойчивости судна


Рассмотрим равнообъемные наклонения судна в поперечной плоскости.
При этом будем полагать, что:
угол наклонения θ является небольшим (до 12°);
участок кривой СС1 траектории ЦВ является дугой круга, лежащей в плоскости наклонения;
линия действия силы плавучести в наклонном положении судна проходит через начальный метацентр m.
Эта формула носит название метацентрической формулы поперечной остойчивости.
При поперечных наклонениях судна на угол, превышающий 12°, пользоваться вышеприведенным выражением не представляется возможным, так как центр тяжести площади наклонной ватерлинии смещается с диаметральной плоскости, а центр величины перемещается не по дуге окружности, а по кривой переменной кривизны, т. е. метацентрический радиус изменяет свою величину.
Диаграмма статической остойчивости строится при помощи пантокарен – графики зависимости плеч остойчивости формы lф от объемного водоизмещения судна и угла крена. Пантокарены конкретного судна строятся в конструкторском бюро для углов крена от 0 до 900 для водоизмещений от порожнего судна до водоизмещения судна в полном грузу (находятся на судне – таблицы кривых элементов теоретического чертежа).
Для построения ДСО необходимо:
на оси абсцисс пантокарен отложить точку, соответствующую объемному водоизмещению судна на момент окончания погрузки;
из полученной точки восстановить перпендикуляр и снять с кривых значения lф для углов крена 10, 200 и т. д.;
вычислить плечи статической остойчивости по формуле:
l = lф – a*sinθ = lф – (Zg – Zc) *sinθ,
построить кривую lф и синусоиду a*sinθ, разности ординат которых являются плечами статической остойчивости l.
Диаграмма статической остойчивости
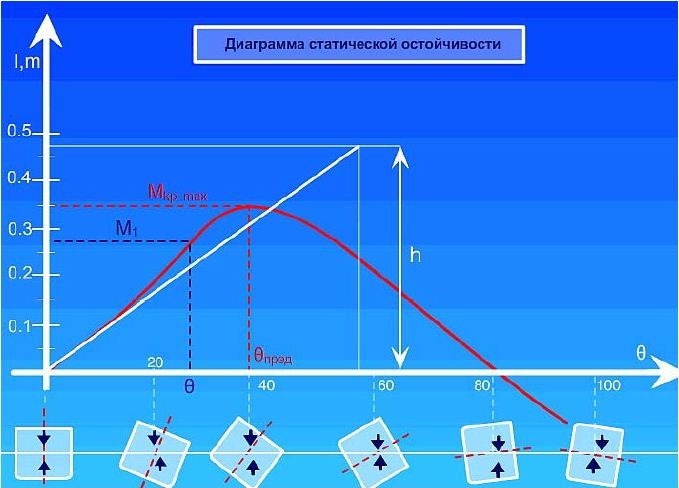
На рис. показаны определенные состояния судна при различных наклонениях:
положение I (θ = 00) соответствует положению статического равновесия (l= 0);
положение II (θ = 200) − появилось плечо статической остойчивости (1 = 0,2м);
положение III (θ = 370) − плечо статической остойчивости достигло максимума (I = 0,35 м);
положение IV (θ = 600) − плечо статической остойчивости уменьшается (I = 0,22 м);
положение V (θ = 830) − плечо статической остойчивости равно нулю. Судно находится в положении статического неустойчивого равновесия, так как даже небольшое увеличение крена приведет к опрокидыванию судна;
положение VI (θ = 1000) − плечо статической остойчивости становится отрицательным и судно опрокидывается.
Начиная с положений, больших, чем положение III, судно будет не способно самостоятельно вернуться в положение равновесия без приложения к нему внешнего усилия.
Пользуясь диаграммой статической остойчивости, можно определить угол крена по известному кренящему моменту М1, возникшему под действием ветра,волнения, смещения груза и т.д. Для его определения проводят горизонтальную линию, выходящую из точки М1, до пересечения с кривой диаграммы, и из полученной точки опускают перпендикуляр на ось абсцисс (θ = 260). Таким же образом решается и обратная задача.
По диаграмме статической остойчивости можно определить величину начальной метацентрической высоты, для нахождения которой необходимо:
из точки на оси абсцисс, соответствующей углу крена 57.3° (один радиан),восстановить перпендикуляр;
из начала координат провести касательную к начальному участку кривой;
измерить отрезок перпендикуляра, заключенный между осью абсцисс и касательной, который в масштабе плеч остойчивости равен метацентрической высоте судна.
Связь между диаграммами статической и динамической остойчивости
Диаграммы статической и динамической остойчивости могут быть преобразованы одна в другую. Алгоритмы построения Диаграммы статической остойчивости рассмотрены в разделах « Построение ДСО по пантокаренам » и « Построение ДСО по типовому варианту ». Алгоритм построение Диаграммы Динамической Остойчивости судна рассмотрен в разделе « Динамическая остойчивость ».
Рисунок 1. Связь между диаграммами статической и динамической остойчивости.
На рисунке 1 изображены диаграмма статической и диаграмма динамической остойчивости, на которой:
1. Точка перегиба диаграммы динамической остойчивости М соответствует максимуму диаграммы статической остойчивости 


2. Ордината диаграммы динамической остойчивости при заданном угле крена, с учетом масштаба, равна площади под кривой плеч статической остойчивости до этого же угла крена.
Связь между диаграммами позволяет оценивать динамическую остойчивость судна на диаграмме статической остойчивости.
Определение плеч статической остойчивости на диаграмме динамической остойчивости
Рисунок 2. Определение плеч статической остойчивости на диаграмме динамической остойчивости
Алгоритм нахождения плеча статической остойчивости на диаграмме динамической остойчивости
Для того, чтобы найти значение плеча статической остойчивости для угла крена θк необходимо:
1. На оси абсцисс из точки, соответствующей заданному углу крена θк, восстановить перпендикуляр до пересечения с кривой плеч динамической остойчивости.
2. В точке пересечения К провести касательную к кривой плеч динамической остойчивости.
3. Из этой же точки провести прямую, параллельную оси абсцисс и на ней отложить отрезок, равный 1 радиану = 57,3°.
4. Из конца отрезка восстановить перпендикуляр до пересечения с касательной.
5. Длина отрезка АВ равняется искомому значению плеча статической остойчивости lст для угла крена θк.
Запас динамической остойчивости на диаграмме статической остойчивости
Динамическая остойчивость определяется величиной работы восстанавливающего момента при наклонении судна до заданного угла. На диаграмме статической остойчивости работа восстанавливающего момента при наклонении до заданного угла соответствует площади между кривой плеч статической остойчивости и осью абсцисс от нуля до заданного угла крена.
В соответствие с требованиями Международного кодекса остойчивости судов в неповрежденном состоянии 2008 года – Кодекс ОСНС 2008 с поправками, принятыми резолюциями MSC.319(89) от 2011 года и MSC.398(95) от 5 июня 2015 года (International Code on Intact Stability — 2008 IS Code) :
1. Площадь под кривой плеч статической остойчивости должна быть не менее 0,055 метро-радиана до угла крена 30° и не менее 0,09 метро-радиана до 40° или угла заливания, если этот угол менее 40°.
2. Кроме того, площадь под кривой между углами крена 30° и 40° или между углами крена 30° и углом заливания, если этот угол менее 40°, должна быть не менее 0,03 метро-радиана.
Рисунок 3. Площади под кривой плеч статической остойчивости.
Алгоритм вычисления площадей на ДСО рассмотрен в разделе « Вычисление площади под кривой плеч статической остойчивости ».
Диаграмма динамической остойчивости
Наклоняющие моменты, действующие на судно, различаются по характеру их приложения к судну.
Например, перекачка жидкого груза на один борт сопровождается ростом кренящего момента настолько медленно, что скорость наклонения судна практически незаметна. В этом случае кренящий момент, измеряемый по его итоговому значению, считается приложенным статически.
Кренящий момент от сильного шквала ветра нарастает до полной величины за единицы или даже доли секунды. За такой период судно не успевает сколько-нибудь значительно изменить посадку и можно считать, что кренящий момент прикладывается к судну внезапно, т.е. уже в начальный момент имеет полную величину. Кренящий момент такого характера называется динамическим, а противодействие такому моменту – динамической остойчивостью.
Рассмотренные два случая являются предельными; реальные кренящие моменты по скорости нарастания нередко занимают промежуточное положение.
Рассмотрим процесс наклонения судна под действием динамического кренящего момента с использованием диаграммы восстанавливающих моментов (рис. 3.10). Допустим, к судну приложен постоянный динамический кренящий момент (Мкр = const).
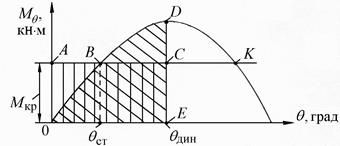 |
Рис. 3.10. К определению динамического угла крена
Графиком действия такого момента на диаграмме будет горизонтальная прямая АК. На участке наклонения от А до В кренящий момент превышает восстанавливающий 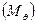
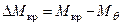
При значении угла qст(угол статического наклонения) кренящий (Мкр) и восстанавливающий (Мq) моменты равны.
На участке В-С нарастающий по величине Мq противодействует двум моментам – 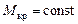
Затем, в силу того, что при qдин имеем 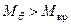
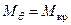
Представленная здесь динамика наклонений судна при приложении динамического кренящего момента является «идеализированной», т.к. не учитывает действия на судно сил, возникающих при его перемещении, в процессе наклонения, относительно воды и воздуха. В реальных условиях, при приложении к судну динамического 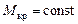
Наклонения судна при приложении к нему динамического момента 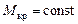
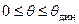
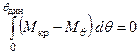 или или 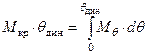 , , | (3.4) |
с учетом того, что 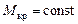
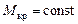
Здесь необходимо отметить, что с использованием диаграммы восстанавливающих моментов задача по определению угла динамического наклонения (qдин) при приложении к судну динамического момента 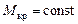
Представленный на рис. 3.10 метод определения qдин обладает наглядностью, но осложняется необходимостью подсчета площади. Другой метод решения задач, связанных с действием динамического кренящего момента, основан на использовании диаграммы динамической остойчивости.
Выражение (3.4) определяет работу 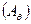
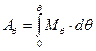 или или 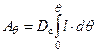 , , |
| где | Dс | – | вес судна при данной загрузке (Dс = const). |
С учетом последнего и, представив работу в виде 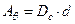
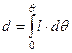 , , | (3.5) |
| где | d | – | называется плечо динамической остойчивости. |
Геометрическая интерпретация зависимости (3.5) дана на рис. 3.11, из которого следует, что плечо динамической остойчивости (d1) при угле θ1, с учетом масштаба, равно площади (S1), ограниченной диаграммой статической остойчивости до этого же угла. В целом диаграмма динамической остойчивости есть интегральная кривая по отношению к диаграмме статической остойчивости.
Интегрирование по формуле (3.5) выполняется по углу, измеряемому в радианах; на диаграмме шкала θ дается в градусах.
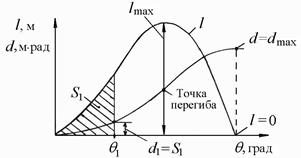 |
Рис. 3.11. Диаграммы статической и динамической остойчивости
Из (3.5), с учетом характера зависимости l(q), следуют ряд соотношений диаграмм статической и динамической остойчивости:
· углу максимума диаграммы статической остойчивости соответствует точка перегиба диаграммы динамической остойчивости (рис. 3.11);
· углу заката диаграммы статической остойчивости соответствует максимум диаграммы динамической остойчивости;
· если на диаграмме динамической остойчивости (рис. 3.12) провести при угле θ1 касательную к кривой d (А – точка касания) и отложить 1 радиан, получим плечо (в масштабе шкалы d) статической остойчивости (l1), соответствующее углу θ1.
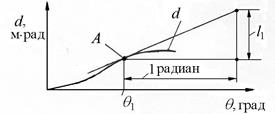 |
Рис.3.12. К определению плеча статической остойчивости
по диаграмме динамической остойчивости
Определение плеч диаграммы динамической остойчивости для ее построения в судовых условиях может быть выполнено с использованием диаграммы статической остойчивости или универсальной диаграммы динамической остойчивости для судна.
Расчет плеч диаграммы динамической остойчивости выполняется в форме табл. 3.1.
Универсальная диаграмма (рис. 3.13) позволяет без расчетов получить плечи диаграммы динамической остойчивости судна при данной его загрузке. Плечо d, определяемое по диаграмме, является результирующей величиной двух составляющих, т.е.
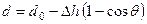 , , | (3.6) |
| где | d0 | – | плечо, соответствующее исходному (фиксированному) значению начальной метацентрической высоты 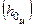 (на рис. 3.13 (на рис. 3.13 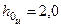 м), м), |
поправка – 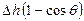
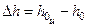
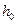
Зависимость (3.6) является интегральной по отношению к зависимости (3.3).
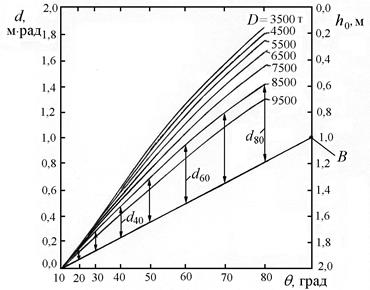 |
Рис. 3.13. Универсальная диаграмма динамической остойчивости
Плечи диаграммы динамической остойчивости для расчетных D и h0 определяются в виде вертикальных отрезков между соответствующей кривой D и лучом, проведенным из начала шкалы d в точку на шкале h0, соответствующую расчетному 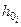
В качестве примера на рис. 3.13 показаны плечи диаграммы динамической остойчивости при D = 8500 т и h0 = 1,0 м (точка B). Значение плеча определяется в масштабе шкалы d.
Дата добавления: 2016-05-16 ; просмотров: 3667 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ