Что общего у сортировки выбором и сортировки вставками
Сортировки и O-нотация
Задача сортировки массива заключается в том, чтобы расставить его элементы в определённом порядке (чаще всего — по неубыванию: каждый элемент должен быть больше или равен предыдущему).
Будет полезно вместе с описанем алгоритмов смотреть их визуализацию.
Сортировка пузырьком
Наш первый подход будет заключаться в следующем: обозначим за \(n\) длину массива и \(n\) раз пройдёмся раз пройдемся по нему, меняя два соседних элемента, если первый больше второго.
Как каждую итерацию максимальный элемент «всплывает» словно пузырек к концу массива — отсюда и название.
После \(i\) шагов алгоритма сортировки пузырьком последние \((i + 1)\) чисел всегда отсортированы, а значит алгоритм работает корректно.
Сортировка выбором
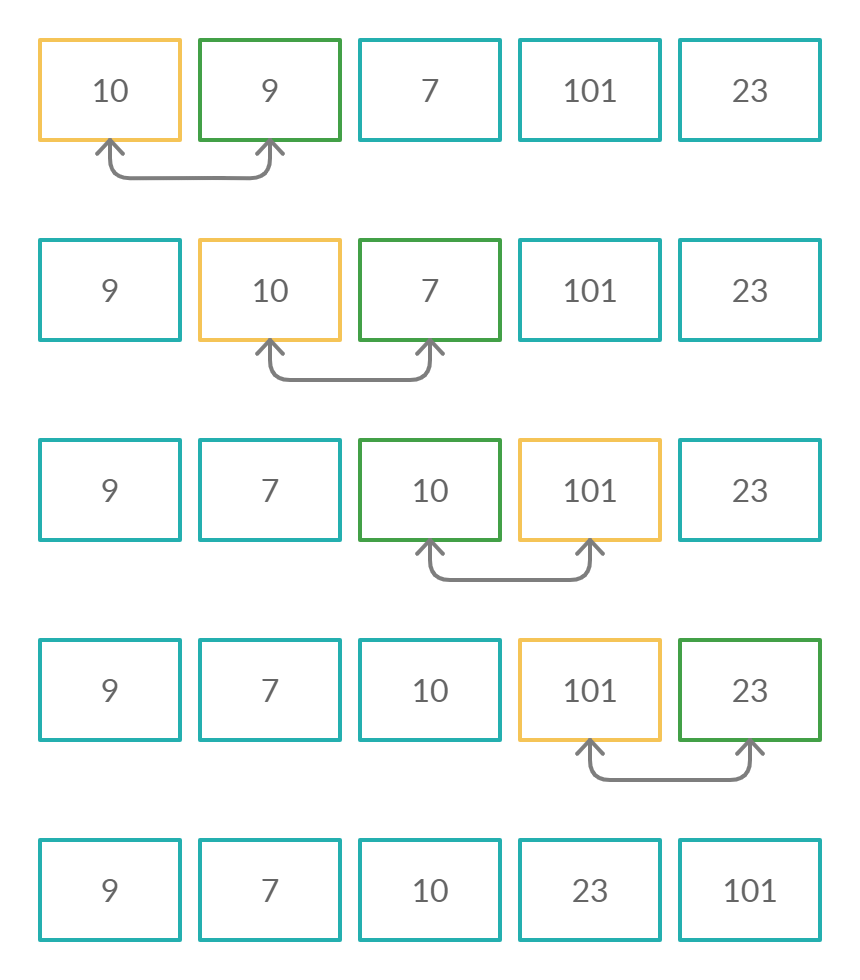
Другим способом является сортировка выбором минимума (или максимума).
Содержательная часть будет выглядеть так:
Сортировка вставками
Определение. Префиксом длины \(i\) будем называть первые \(i\) элементов массива.
Сортировка подсчетом
Предыдущие три алгоритма работали с массивами, в которых лежат абсолютно любые объекты, которые можно сравнивать: любые числа, строки, пары, другие массивы — почти все что угодно.
Но особых случаях, когда элементы принадлежат какому-то маленькому множеству, можно использовать другой алгоритм — сортировку подсчетом.
О-нотация
Часто требуется оценить, сколько времени работает алгоритм. Но тут возникают проблемы:
Зачастую основной задачей программиста становится оптимизировать алгоритм, выполнение которого займёт тысячи лет, до какого-нибудь адекватного времени работы. Поэтому хотелось бы уметь предсказывать, сколько времени займёт выполнение алгоритма ещё до того, как мы его запустим.
Для этого сначала попробуем оценить число операций в алгоритме. Возникает вопрос: какие именно операции считать. Как один из вариантов — учитывать любые элементарные операции:
Упражнение. Попробуйте посчитать точное число сравнений и присваиваний в сортировках пузырьком, выбором, вставками и подсчетом в худшем случае (это должна быть какая формула, зависящая от \(n\) — длины массива).
В таких обозначениях можно сказать, что
Все рассуждения про то, сколько операций в swap или считать ли отдельно присваивания, сравнения и циклы — отпадают. Каков бы ни был ответ на эти вопросы, они меняют ответ лишь на константу, а значит асимптотическое время работы алгоритма никак не меняется.
Упражнение. Найдите асимптотическое время работы данных функций:
Упражнение. Найдите лучшее время работы алгоритмов, решающих данные задачи:
Сортировки за \(O(n \log n)\)
Сортировка очень часто применяется как часть решения олимпиадных задач. В таких случаях обычно не пишут её заново, а используют встроенную.
Сортировка слиянием
А можно ли быстрее?
Это называется метод двух указателей — так как мы двигаем два указателя first и second одновременно слева направо по каким-то правилам. Обычно его используют на одном отсортированном массиве.
Давайте разберем еще примеры.
Слияние
Еще пример двух указателей на нескольких массивах.
Пусть первый указатель будет указывать на начало первого массива, а второй, соответственно, на начало второго. Из двух текущих элементов, на которые указывают указатели, выберем наименьший и положим на соответствующую позицию в новом массиве, после чего сдвинем указатель. Продолжим этот процесс пока в обоих массивах не закончатся элементы. Тогда код будет выглядеть следующим образом:
Сортировка слиянием
Пусть у нас есть какой-то массив.
Так сколько же работает это решение?
Количество инверсий
Найти количество инверсий в данной перестановке.
Очевидно, что эта задача легко решается обычным перебором двух индексов за \(O(n^2)\) :
Заметим, что мы уже знаем количество инверсий в левой половине и в правой половине массива. Осталось лишь посчитать число инверсий, где одно число лежит в левой половине, а второе в правой половине. Как же их посчитать?
Давайте подробнее рассмотрим операцию merge левой и правой половины (которую мы ранее заменили на вызов встроенной функции merge). Первый указатель указывает на элемент левой половины, второй указатель указывает на элемент второй половины, мы смотрим на минимум из них и этот указатель вдигаем вправо.
Значит в тот момент, когда мы добавляем число \(A\) из левой половины, к ответу достаточно прибавить индекс второго указателя (минус начало правой половины). Так мы учтем все инверсии между половинами.
Быстрая сортировка
Быстрая сортировка заключается в том, что на каждом шаге мы находим опорный элемент, все элементы, которые меньше его кидаем в левую часть, остальные в правую, а затем рекурсивно спускаемся в обе части.
Существуют несколько выходов из этой ситуации :
Давайте делить массив не на две, а на три части(меньше, равны, больше).
Чтобы избавиться от проблемы с максимумом/минимумом в середине, давайте брать случайный элемент.
Давайте поймем, что в быстрой сортировке мы можем узнать, сколько элементов меньше данного, тогда рассмотрим три случая
Сравнение алгоритмов сортировки
В данной статье рассматриваются алгоритмы сортировки массивов. Для начала представляются выбранные для тестирования алгоритмы с кратким описанием их работы, после чего производится непосредственно тестирование, результаты которого заносятся в таблицу и производятся окончательные выводы.
Алгоритмы сортировок очень широко применяются в программировании, но иногда программисты даже не задумываются какой алгоритм работает лучше всех (под понятием «лучше всех» имеется ввиду сочетание быстродействия и сложности как написания, так и выполнения).
В данной статье постараемся это выяснить. Для обеспечения наилучших результатов все представленные алгоритмы будут сортировать целочисленный массив из 200 элементов. Компьютер, на котором будет проводится тестирование имеет следующие характеристики: процессор AMD A6-3400M 4×1.4 GHz, оперативная память 8 GB, операционная система Windows 10 x64 build 10586.36.
Для проведения исследования были выбраны следующие алгоритмы сортировки:
Selection sort (сортировка выбором) – суть алгоритма заключается в проходе по массиву от начала до конца в поиске минимального элемента массива и перемещении его в начало. Сложность такого алгоритма O(n2).
Bubble sort (сортировка пузырьком) – данный алгоритм меняет местами два соседних элемента, если первый элемент массива больше второго. Так происходит до тех пор, пока алгоритм не обменяет местами все неотсортированные элементы. Сложность данного алгоритма сортировки равна O(n^2).
Insertion sort (сортировка вставками) – алгоритм сортирует массив по мере прохождения по его элементам. На каждой итерации берется элемент и сравнивается с каждым элементом в уже отсортированной части массива, таким образом находя «свое место», после чего элемент вставляется на свою позицию. Так происходит до тех пор, пока алгоритм не пройдет по всему массиву. На выходе получим отсортированный массив. Сложность данного алгоритма равна O(n^2).
Quick sort (быстрая сортировка) – суть алгоритма заключается в разделении массива на два под-массива, средней линией считается элемент, который находится в самом центре массива. В ходе работы алгоритма элементы, меньшие чем средний будут перемещены в лево, а большие в право. Такое же действие будет происходить рекурсивно и с под-массива, они будут разделяться на еще два под-массива до тех пор, пока не будет чего разделать (останется один элемент). На выходе получим отсортированный массив. Сложность алгоритма зависит от входных данных и в лучшем случае будет равняться O(n×2log2n). В худшем случае O(n^2). Существует также среднее значение, это O(n×log2n).
Comb sort (сортировка расческой) – идея работы алгоритма крайне похожа на сортировку обменом, но главным отличием является то, что сравниваются не два соседних элемента, а элементы на промежутке, к примеру, в пять элементов. Это обеспечивает от избавления мелких значений в конце, что способствует ускорению сортировки в крупных массивах. Первая итерация совершается с шагом, рассчитанным по формуле (размер массива)/(фактор уменьшения), где фактор уменьшения равен приблизительно 1,247330950103979, или округлено до 1,3. Вторая и последующие итерации будут проходить с шагом (текущий шаг)/(фактор уменьшения) и будут происходить до тех пор, пока шаг не будет равен единице. Практически в любом случае сложность алгоритма равняется O(n×log2n).
Для проведения тестирования будет произведено по 5 запусков каждого алгоритма и выбрано наилучшее время. Наилучшее время и используемая при этом память будут занесены в таблицу. Также будет проведено тестирование скорости сортировки массива размером в 10, 50, 200 и 1000 элементов чтобы определить для каких задач предназначен конкретный алгоритм.
Полностью неотсортированный массив:
Частично отсортированный массив (половина элементов упорядочена):
Результаты, предоставленые в графиках:
В результате проведенного исследования и полученных данных, для сортировки неотсортированного массива, наиболее оптимальным из представленных алгоритмов для сортировки массива является быстрая сортировка. Несмотря на более длительное время выполнения алгоритм потребляет меньше памяти, что может быть важным в крупных проектах. Однако такие алгоритмы как сортировка выбором, обменом и вставками могут лучше подойти для научных целей, например, в обучении, где не нужно обрабатывать огромное количество данных. При частично отсортированном массиве результаты не сильно отличаются, все алгоритмы сортировки показывают время примерно на 2-3 миллисекунды меньше. Однако при сортировке частично отсортированного массива быстрая сортировка срабатывает намного быстрее и потребляет меньшее количество памяти.
Алгоритмы сортировки
Алгоритм сортировки — это алгоритм для упорядочивания элементов в списке.
Виды алгоритмов сортировки
Сортировка пузырьком / Bubble sort
Сортировка пузырьком — это простейший и один из самых известных алгоритмов сортировки. Идея заключается в последовательном сравнении значений соседних элементов. Если текущий элемент больше следующего, меняем их местами. Алгоритм необходимо повторять до тех пор, пока массив не будет отсортирован.
Плюсы и минусы
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.
Пример реализации на Kotlin:
Сортировка перемешиванием / Shaker (cocktail, ripple, shuffle, shuttle) sort
Также известна как шейкерная или коктейльная сортировка.
Общая идея алгоритма:
Пример реализации на Kotlin:
Сложность у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше (обычно менее чем в два раза быстрее).
Сортировка расчёской / Comb sort
Достигается это тем, что вместо сравнения соседних элементов, сравниваются элементы на достаточно большом расстоянии друг от друга, постепенно уменьшая это расстояние. Сначала разрыв между элементами берётся максимальный, т.е. на единицу меньше, чем размер массива. Затем на каждой итерации расстояние уменьшается путём деления расстояния на фактор уменьшения. Так продолжается до тех пор, пока разность индексов сравниваемых элементов не достигнет единицы. Тогда сравниваются уже соседние элементы как и в сортировке пузырьком, но эта итерация будет последней.
Пример реализации на Kotlin:
Сортировка вставками / Insertion sort
Общая идея алгоритма:
Пример реализации на Kotlin:
Сортировка Шелла / Shell sort
Первоначально было предложено расчитывать расстояние между сравниваемыми элементами следующим образом:
Существуют и другие последовательности.
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | зависит от выбранных шагов (d) | O(n 2 ) или O(n log 2 n) (зависит от выбранных шагов) |
| Память | O(1) |
Сортировка выбором / Selection Sort
Общая идея алгоритма:
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n 2 ) | O(n 2 ) | O(n 2 ) |
| Память | O(1) |
Быстрая сортировка / Quick Sort
Общая идея алгоритма:
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n log n) | O(n 2 ) |
| Память | O(n) |
Сортировка слиянием / Merge sort
Общая идея алгоритма:
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | O(n log n) | O(n log n) |
| Память | O(n) |
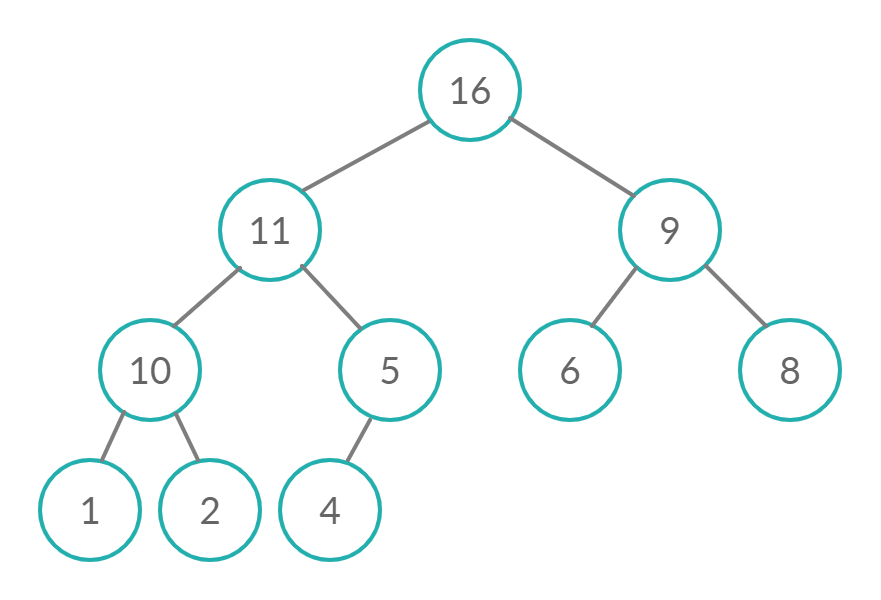
Пирамидальная сортировка / Heap sort
Общая идея алгоритма:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | O(n log n) | O(n log n) или O(n) (при одинаковых ключах) |
| Память | O(1) |
Сортировка подсчётом / Counting sort
Общая идея алгоритма (простой вариант):
Пример реализации на Kotlin:
Блочная (карманная, корзинная) сортировка / Bucket sort
Общая идея алгоритма:
Пример реализации на Kotlin:
Поразрядная (цифровая) сортировка / Radix sort
Перед началом сортировки необходимо знать:
Общая идея алгоритма:
Пример реализации на Kotlin:
Битонная сортировка / Bitonic sort
Общая идея алгоритма:
Чтобы превратить произвольную последовательность в битонную, нужно:
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(log 2 (n) | O(log 2 (n) | O(log 2 (n) |
| Память | O(log 2 (n) |
Timsort
Общая идея алгоритма:
Пример реализации на Kotlin:
Гибридные сортировки
Как все уже знают, в основу сортировки могут быть положены обмены, вставки, выбор, слияние и распределение.
Но если в алгоритме комбинируются разные методы, то тогда он относится к классу гибридных сортировок.

Статья написана при поддержке компании EDISON.
Мы очень любим теорию алгоритмов! 😉
Давайте быстро вспомним, какие классы бывают у алгоритмов сортировок и в чём особенности каждого из них.
Сортировки обменами

Элементы массива попарно сравниваются друг с другом и производятся обмены для неупорядоченных пар.
Самым эффективным представителем этого класса является легендарная быстрая сортировка.
Сортировки вставками

Элементы из неотсортированной части массива вставляются на свои места в отсортированной области.
Из этого класса чаще всего используется сортировка простыми вставками. Хотя этот алгоритм имеет среднюю сложность O(n 2 ), эта сортировка очень быстро работает с почти упорядоченными массивами — на них сложность достигает O(n). Кроме того, эта сортировка является одним из лучших вариантов для обработки малых массивов.
Сортировка с помощью двоичного дерева поиска тоже относится к данному классу.
Сортировки выбором

В неупорядоченной области выбирается минимальный/максимальный элемент, который переносится в конец/начало неотсортированной части массива.
Сортировки простым выбором работают весьма медленно (в среднем O(n 2 )), но в этом классе есть непростая сортировка кучей (она же пирамидальная сортировка), которая имеет сложность по времени O(n log n) — и, что очень ценно, у этой сортировки нет вырожденных случаев, каковы бы ни были входящие данные. Лучших случаев для входящих данных, у этой сортировки, кстати, тоже нет.
Сортировки слиянием
В массиве берутся отсортированные области и осуществляется их слияние, то есть отсортированные подмассивы поменьше объединяются в общий отсортированный подмассив побольше.
Если два подмассива отсортированы, то их объединение — легко реализуемая и быстрая по времени операция. Обратной стороной медали является то, что на слияние почти всегда требуются расходы на дополнительную память O(n) — хотя известно крайне небольшое количество особо изощрённых вариантов сортировок со слиянием, где расходы по памяти O(1).
Сортировки распределением
Элементы массива распределяются и перераспределяются по классам до тех пор, пока массив не примет отсортированное состояние.
Элементы разбрасываются по группам или в зависимости от их значения (так называемые сортировки подсчётом) или в зависимости от значения отдельных разрядов (это уже поразрядные сортировки).
Вёдерная сортировка также относится к данному классу.
Особенностью сортировок распределением является то, что они или вообще не используют попарные сравнения элементов между собой, или таковые сравнения присутствуют в незначительной мере. Поэтому сортировки распределением часто опережают по скорости, например, быструю сортировку. С другой стороны, сортировки распределением часто требуют много дополнительной памяти, так как группы постоянно перераспределяемых элементов надо где-то хранить.
Очень часты ведутся споры о том, какая сортировка является самой лучшей, но в том-то и дело, что идеального алгоритма на все случаи жизни нет и быть не может. Например, быстрая сортировка действительно очень быстрая (но не самая быстрая) в большинстве ситуаций, но и для неё попадаются вырожденные случаи, в которых происходит крах. Сортировка простыми вставками медленная, но для почти упорядоченных массивов запросто обойдёт другие алгоритмы. Сортировка кучей работает вполне быстро при любых входящих данных, но не настолько быстро как другие сортировки при определённых условиях и нет возможности пирамиду ускорить. Сортировка слиянием медленнее, чем быстрая сортировка, однако если в массиве есть отсортированные подмассивы, то быстрее произвести их слияние, чем досортировывать быстрой сортировкой. Если в массиве много повторяющихся элементов или сортируем строки, то, скорее всего, сортировка распределением — наилучший вариант. Каждый метод особенно хорош в своей самой благоприятной ситуации.
И тем не менее, программисты продолжают изобретать самые быстрые в мире сортировки, синтезируя наиболее эффективные методы из разных классов. Давайте поглядим, насколько успешно у них это выходит.
Поскольку в статье упоминается много нетривиальных алгоритмов, я лишь кратко освещаю основные принципы их работы, не перегружая статью анимациями и подробными объяснениями. В дальнейшем будут отдельные статьи, где будут и «мультики» для каждого алгоритма и обстоятельно разобранные тонкие нюансы.
Вставка + слияние
Чисто эмпирический вывод гласит о том, что в гибридах чаще всего используется слияние и/или вставки. В большинстве сортировок встречается или тот или другой метод, а то и оба вместе. И этому есть логическое объяснение.
Изобретатели сортировок зачастую стремятся к созданию параллельных алгоритмов, одновременно упорядочивающих разные участки массива. Лучший способ как поступить с несколькими отсортированными подмассивами — это произвести их слияние — так будет быстрее всего.
В современных алгоритмах часто используется рекурсия. При рекурсивном спуске массив делится обычно на две части, на самом нижнем уровне происходит упорядочивание массива. При возвращении на более высокие уровни рекурсии при этом ставится вопрос объединения отсортированных на нижних уровнях подмассивах.
Что касается вставок, то в гибридных алгоритмах на определённых этапах часто получаются примерно упорядоченные подмассивы, которые лучше всего приводить к окончательному упорядочиванию именно с помощью вставок.
В этой группе собраны гибридные сортировки, в которых есть и слияние и вставки, причём эти методы применяются очень даже по-разному.
Сортировка слиянием-вставкой :: Merge-insertion sort
Алгоритм Форда-Джонсона :: Ford-Johnson algorithm
Слияние + вставки

Очень древний способ, аж 1959 года. Подробно описан в бессмертном труде Дональда Кнута «Искусство программирования», Том 3 «Сортировка и поиск», глава 5 «Сортировка», раздел 5.3 «Оптимальная сортировка», подраздел «Сортировка с минимальным числом сравнений», часть «Сортировка посредством вставок и слияния».
Сортировка сейчас не имеет практического значения, однако интересна тем, кто любит теорию алгоритмов. Рассмотрена задача нахождения способа, как с наименьшим количеством сравнений отсортировать n элементов. Предлагается нетривиальная эвристическая модификация сортировки вставкой (такой вставки Вы больше нигде не встретите) с использованием чисел Якобсталя, для того чтобы количество сравнений свести к минимуму. На сегодняшний день к тому же известно, что это не самый оптимальный вариант и можно ещё более ловко извернуться и обойтись ещё меньшим количеством сравнений. В общем, эталонная академическая сортировка — практической пользы нет, но для ценителей жанра разбирать подобные хитромудрости с алгебраическим уклоном одно удовольствие.
Сортировка Тима :: Timsort
Вставки + слияние

Автор Тим Петерс лет 15 назад и сейчас
Эту сортировку на Хабре вспоминают очень часто.
Тезисно: в массиве ищутся почти упорядоченные небольшие подмассивы, для которых применяется сортировка вставками. Затем эти подмассивы объединяются с помощью слияния.
Слияние в TimSort — наиболее интересная часть: классическое восходящее слияние дополнительно оптимизировано для разных ситуаций. Например, известно, что слияние более эффективно проходит, если соединяемые подмассивы примерно одинаковы по размеру. В TimSort если размеры сильно отличаются, то после дополнительных действий происходит уравнивание (можно сказать, что из большего подмассива часть элементов «перетечёт» в меньший, после чего слияние продолжится в стандартном режиме). Также предусмотрены разные коварные ситуации — например, если в одном подмассиве все элементы будут меньше чем в другом. В этом случае сравнение элементов из обоих подмассивов будет проходить вхолостую. Модифицированная процедура слияния вовремя «заметит» такое нежелательное развитие событий и если с помощью бинарного поиска «убедится» в пессимистичном варианте, то произойдёт переключение на более оптимальный вариант обработки.
В среднем эта сортировка работает чуть медленнее чем QuickSort, однако если входящий массив содержит достаточное количество упорядоченных подпоследовательностей элементов, то скорость существенно повышается и тут TimSort идёт впереди планеты всей.
Сортировка блочным слиянием :: Block merge sort
Вики-сортировка :: Wiki-sort
Сортировка святого Грааля :: Grailsort
Вставки + слияние + вёдра

Анимация сортировки блочным слиянием из Википедии.
Это весьма свежий (2008 год) и в то же время очень перспективный алгоритм. Дело в том, что относительно весомой проблемой слияния является затраты на дополнительную память. Обычно, там где слияние — там и сложность по памяти O(n).
Но WikiSort устроен так, что слияние происходит без использования дополнительной памяти — среди сортировок слиянием в этом плане это очень редкий экземпляр. Кроме того алгоритм является стабильным. Ну и, если обычная сортировка слиянием имеет лучшую алгоритмическую скорость O(n log n), то у вики-сортировки этот показатель равен O(n). До недавнего времени считалось, что сортировка слиянием с таким набором характеристик невозможна в принципе, но китайские программисты всех удивили.
Алгоритм сильно сложен, чтобы его пояснить в паре предложений. Но когда-нибудь о нём напишу отдельную хабрастатью.
Изначально алгоритм безлико назывался Block Merge Sort однако с лёгкой руки Тима Петерса, который подробно изучал сортировку (на предмет того, стоит ли некоторые её идеи перенести в TimSort) к ней прилепилось название WikiSort.
Безвременно ушедший от нас хабраюзер Mrrl самостоятельно несколько лет работал над сортировкой слиянием которая была бы одновременно быстрой при любых входящих данных, экономичной по памяти и устойчивой. Его творческие поиски увенчались успехом и разработанный алгоритм он несколько позже назвал сортировкой святого Грааля (так как она удовлетворяет всем высоким требованиям «идеальной сортировки»). Большинство идей этого алгоритма похожи на то, что реализовано в WikiSort, хотя эти сортировки не идентичны и разработаны независимо друг от друга.
Сортировка с помощью хеш-таблицы :: Hash table sort
Распределение + вставки + слияние
Массив рекурсивно делится пополам, пока количество элементов в получаемых подмассивах не достигнет некоторого порогового значения. На самом нижнем уровне рекурсии происходит приблизительное распределение (с использованием хеш-таблицы) и сортировка подмассива вставками. Затем происходит рекурсивный возврат на более высокие уровни, отсортированные половинки объединяются посредством слияния.
Чуть более подробно об этом алгоритме я рассказывал месяц назад.
Быстрая сортировка как основная
После слияния и вставки третье место в гибридном хит-параде прочно удерживает всеми любимая быстрая сортировка.
Это очень эффективный алгоритм, однако и для него есть вырожденные случаи. Некоторые изобретатели пытаются сделать QuickSort полностью неуязвимой к любым плохим входящим данным и предлагают её дополнить сильными идеями из других сортировок.
Интроспективная сортировка :: Introsort, Introspective sort, std::sort
Быстрая + куча + вставки

Сортировка кучей работает несколько медленнее, чем быстрая сортировка, но при этом у неё в отличие от QuickSort нет вырожденных случаев — средняя, лучшая и худшая алгоритмическая сложность по времени O(n log n).
Поэтому Дэвид Мюссер предложил обезопасится при быстрой сортировке — если наблюдается слишком большой уровень вложенности, то это расценивается как атака на систему, которой подсунули «плохой» массив. Происходит переключение на сортировку кучей, которая не мегабыстро, но и не медленно справится входящими данными.
Многомерная сортировка :: Multikey sort
Порязрядная быстрая сортировка :: Radix quick sort
Быстрая + разряды
Быстрая сортировка, только сравниваются друг с другом не значения элементов массива, а их отдельные разряды (сначала таким образом упорядочиваем старшие разряды, от них двигаемся к младшим).
Или так — это поразрядная сортировка по старшим разрядам, упорядочивание внутри очередного разряда осуществляется по алгоритму быстрой сортировки.
Сортировка разбросами :: Spreadsort
Быстрая + слияние + вёдра + разряды
Гештальт из быстрой сортировки, сортировки слиянием, вёдерной сортировки и поразрядной сортировки.
В двух словах не объяснить. Этот алгоритм подробно разберём в одной из следующих статей.
Прочие гибриды
Сортировка подсчётом/деревом :: Tree-counting sort
Подсчёт + дерево
Алгоритм, предложенный хабрапользователем AlexanderUsatov. Сортировка подсчётом, количества подсчитываемых ключей хранятся в сбалансированном дереве.
J-сортировка :: J-sort
Куча + вставки
Про эту сортировку я уже писал 5 лет назад. Всё достаточно просто — сначала в массиве нужно однократно построить невозрастающую кучу, а затем сделать с точностью до наоборот — однократно построить неубывающую. В результате первой операции минимум окажется на первом месте массива, а небольшие элементы в целом значительно переместятся в начало. Во втором случае максимум окажется на последнем месте, а крупные элементы мигрируют в направлении конца массива. В общем получаем почти отсортированный массив, с которым мы что делаем? Правильно — досортировываем вставками.
Ссылки