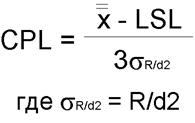Что обозначает в статистических методах индекс срк
Характеристики процесса. Оценка воспроизводимости процессов. Индекс пригодности, определяемый как допуск, деленный на пригодность процесса без учета его центровки
Страницы работы
Содержание работы
n Стабильность процесса – состояние процесса, когда в нем отсутствуют особые причины изменчивости
n Возможность процесса – степень соответствия результатов стабильного процесса установленным требованиям
Оценка стабильности и воспроизводимости (Инструментарий SPC)
НЕстабильность – контрольные карты
Воспроизводимость – индексы Ср, Срк, Рр, Ррк
Оценка воспроизводимости процессов
Воспроизводимость, или другими словами, способность процесса удовлетворить допуск, в свою очередь, характеризуется двумя величинами – настройкой и разбросом. Эти величины используются при расчете индексов, которые называются индексами (воспроизводимости) возможности процесса и которые говорят о способности процесса удовлетворять установленным требованиям, т.е. допуску.
Индексы Ср и Срк применяются для оценки стабильного процесса.
Индексы Рр и Ррк используются для оценки нестабильного процесса.
Ср – допуск, деленный на воспроизводимость процесса без учета его центровки
Ср – говорит о потенциальных возможностях процесса, он показывает сколько раз по 6 сигм может уложиться в границы допуска.
Если Ср=1 то разброс процесса (шестисигмовый интервал) равен полю допуска. Если центр настройки процесса находится точно по центру поля допуска, то вероятность появления несоответствий составит 0.0027, или 0,27%.
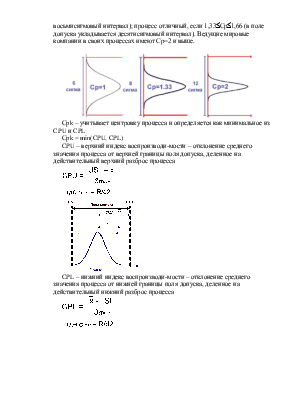
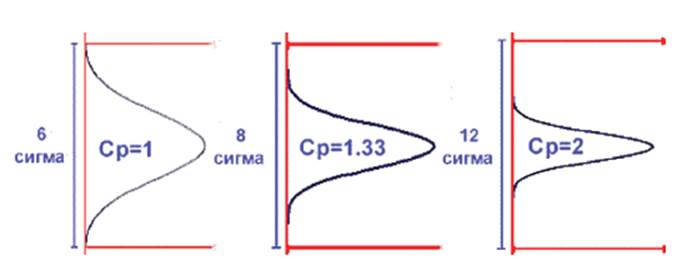
Считается, что процесс с точки зрения Ср удовлетворителен, если Ср=1; процесс хороший, если 1£Ср£1,33 (в поле допуска укладывается восьмисигмовый интервал); процесс отличный, если 1,33£Ср£1,66 (в поле допуска укладывается десятисигмовый интервал). Ведущие мировые компании в своих процессах имеют Ср=2 и выше.
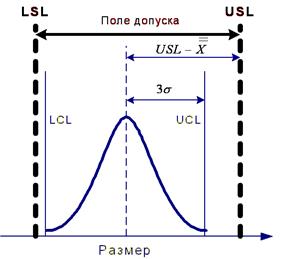
Сpk – учитывает центровку процесса и определяется как минимальное из CPU и CPL
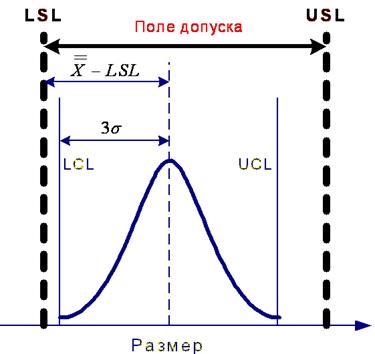
CPU – верхний индекс воспроизводи-мости – отклонение среднего значения процесса от верхней границы поля допуска, деленное на действительный верхний разброс процесса
CPL – нижний индекс воспроизводи-мости – отклонение среднего значения процесса от нижней границы поля допуска, деленное на действительный нижний разброс процесса
Сpk – показывает, сколько раз по 3s укладывается до ближайшей границы допуска
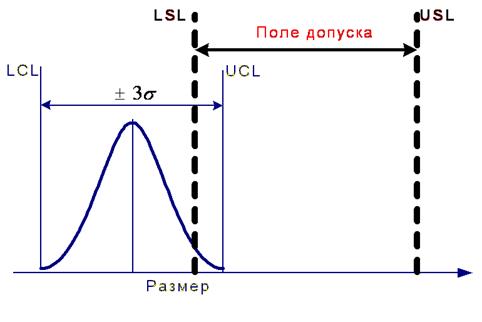
Рассмотрим соотношение этих двух индексов. Из приведенных рисунков очевидно, что Ср не может быть меньше Срк, т.к. Срк – эти минимальная величина верхнего и нижнего индексов воспроизводимости. Следовательно, наибольшим Срк будет, когда центр настройки процесса совпадает с центром поля допуска. В этом случае Срк будет равняться Ср. Во всех остальных случаях Срк будет меньше. Важное отличие Срк от Ср – то, что Срк может быть отрицательным. Это возможно в случае, когда центр настройки процесса находится за пределами поля допуска.
Pp – индекс пригодности, определяемый как допуск, деленный на пригодность процесса без учета его центровки
Ppk – учитывает центровку процесса и определяется как минимальное из
(USL – x) /3ss и (x – LSL) /3ss
Индексы были впервые внедрены японскими фирмами, а в 1986 году применены в США фирмой «Форд моторс» во взаимоотношениях с поставщиками и с тех пор успешно применяются во всем мире.
Для понимания рассмотрим классический пример с постановкой машины в гараж. В примере ширина гаража является допустимым разбросом (допуском), а ширина машины – фактическим разбросом.
Если индекс воспроизводимости равен единице, то фактический разброс (т.е. 6σ) равен допуску. В этом случае вы поставите машину в гараж, но выйти из неё уже не сможете. Поэтому, хотя формально равенство допустимого и фактического разброса является показателем стабильности процесса, эта цифра является неприемлемой в реальном производстве, поскольку при малейших отклонениях она может стать меньше единицы.
Машину невозможно поставить в гараж, если ширина гаража меньше ширины машины. Другими словами, если фактический разброс больше допустимого и значение Cp меньше единицы, процесс не является воспроизводимым.
И, если допустимый разброс больше чем фактический разброс 6σ (ширина машины меньше ширины гаража), то все в порядке.
Индексы пригодности процесса
Существуют много методов оценки качества, однако как только производственный процесс становится управляемым, возникает следующий вопрос: «в какой степени долговременное поведение процесса удовлетворяет техническим условиям и целям, поставленным руководством?» Рассмотрим, как мы можем оценить пригодность процесса с помощью осмысленных показателей.
Итак, следует различать управляемый и неуправляемый процесс. Заметим, что нет смысла изучать пригодность производственного процесса, если он не управляем. Следовательно, первый шаг к организации высококачественного процесса производства состоит в том, чтобы сделать процесс управляемым.
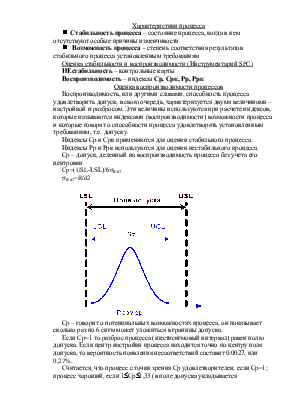
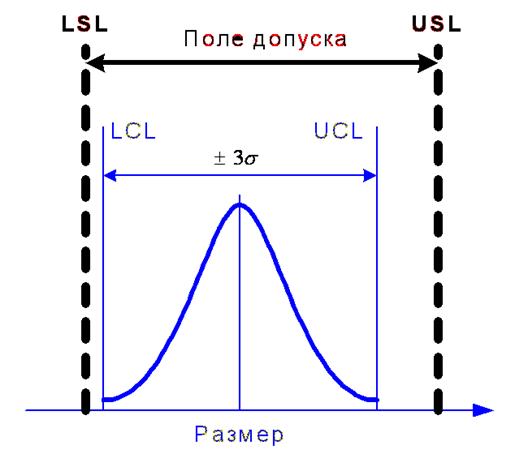
Если процесс управляем, то можно ставить вопрос о его пригодности. В случае примера с поршневыми кольцами, заметим, что если дана выборка определенного объема, то можно оценить стандартное отклонение процесса, то есть сигма производства поршневых колец. Затем можно построить гистограмму распределения диаметров поршневых колец. Если распределение диаметров нормальное, то можно сделать выводы о доле поршневых колец, попадающих в границы допуска (см. рис.1).
Рисунок 1. Нормальное распределение, границы допуска
Индексы пригодности процесса
Общеупотребительными индексами пригодности процесса являются индексы пригодности (Cp и Cpk), т.к. они достаточно полно отражают отношения технически возможных отклонений (размаха процесса) к ±3 сигма пределам от первоначальных спецификаций.
Для вычислений нам потребуется стандартное отклонение Сигма
Вычисляем средний размах
Вычисляем сигма 
Замечание: стандартное отклонение наблюдений не равно стандартному отклонению средних всех выборок, которое является результатом деления стандартного отклонения на квадратный корень из n (объем выборки).
НГД, ВГД (нижняя и верхняя границы допуска). Обычно технические условия задают некий диапазон допустимых значений. Разность между НГД и ВГД называется размахом допуска.
Формулы индексов пригодности
Потенциальная пригодность (Cp). Это простейший и самый естественный показатель пригодности производственного процесса. Он определяется как отношение размаха допуска к размаху процесса; при использовании границ ±3 сигма данный показатель можно выразить в виде 
Нижняя/верхняя потенциальная пригодность (Cpl, Cpu). Недостаток показателя Cp состоит в том, что он может дать неверную информацию о производственном процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован.
Для пояснения можно провести некоторую аналогию: Вы стреляете по мишени из ружья. Если попадаете точно «в яблочко», то это высокий Сp; если же прицел смещен, и Вы все время попадаете в узкую область, лежащую далеко от центра, то Сp будет высоким при низкой потенциальной пригодности процесса.
Нецентрированность (смещенность) процесса производства можно выразить следующим образом. Сначала можно вычислить верхний и нижний показатели пригодности, чтобы отразить отклонение наблюдаемого среднего процесса от НГД и ВГД. Приняв в качестве размаха процесса границы ±3 сигма, вычислим следующие показатели:
Подтвержденное качество (Cpk). Наконец, Cp можно скорректировать, внеся поправку на нецентрированность посредством вычисления 
Высокий Cpk будет только в том случае, когда цель достигнута при минимальном отклонении от среднего.
Индексы производительности процесса
При контроле процесса с помощью карт контроля качества (например, X- или R-карты) часто бывает полезно вычислять показатели пригодности процесса. Когда набор данных состоит из нескольких выборок, то можно вычислить два разных показателя изменчивости. Один из них – обычное стандартное отклонение для всех наблюдений, не принимающее в расчет, что данные состоят из нескольких выборок; другой показатель оценивает собственный разброс процесса по изменчивости внутри выборки. Если при стандартных вычислениях пригодности используется общая изменчивость процесса, то полученные показатели обычно называют показателями качества процессам Pp и Ppk (process performance) (поскольку они описывают фактическое поведение процесса).
Индекс производительности процесса по существу пытается подтвердить то, что полученная Вами выборка способна удовлетворить требования клиентов. Производительность процесса используется только, когда контроль не может быть осуществлен (Например, при пробном производстве небольшого числа изделий).
Индекс Cpk краткосрочный, а Ppk – долгосрочный. Cpk говорит, что Ваш процесс сможет делать в будущем. Ppk говорит, насколько хорошо процесс был представлен в прошлом. Вы не можете использовать этот показатель в будущем, как Cpk, потому что процесс не подвергается непрерывному контролю. Значения Cpk и Ppk стремятся почти к одному и тому же значению, когда процесс статистически контролируется. Это происходит из-за того, что в этом случае сигма =стандартное отклонение. Если контроль не осуществляется, значения, естественно, будут различными, разница, возможно, будет достаточно велика.
Реалистичней использовать Pp и Ppk, чем Cp или Cpk, так как дисперсия процесса не сочетается с разбиением на выборки. Однако, Cp и Cpk могут быть очень полезны при определении попадания пригодности процесса в определенные границы. Это даст Вам наилучший сценарий развития существующего процесса.
Формулы индексов производительности
где 
Негауссовские распределения
Рассмотрим что делать, если распределение соответствующего параметра качества или переменной (например, диаметров поршневых колец) не является нормальным.
Если того требует поставленная задача, гистограмму можно аппроксимировать отличным от нормального распределением и вычислить показатели пригодности с помощью метода процентилей. Для всех распределений можно также вычислить таблицы ожидаемых частот, ожидаемое число наблюдений, выходящих за рамки технических условий, и построить графики квантиль-квантиль и вероятность-вероятность.
Негауссовские индексы пригодности
где M – медиана (50 процентиль) соответствующего распределения,
Up и Lp – 99.865 и 0.135 процентили соответственно.
Обратите внимание, что значения Up и Lp могут быть другими, если размах процесса задан другими границами (например, ±2 сигма).
Что обозначает в статистических методах индекс срк
ГОСТ Р 50779.46-2012/ISO/TR 22514-4:2007
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Оценка показателей воспроизводимости и пригодности процесса
Statistical methods. Process management. Part 4. Process capability and performance estimation
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии документа, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1273-ст
Наименование настоящего стандарта изменено относительно наименования указанного международного документа для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
6 ПЕРЕИЗДАНИЕ. Август 2020 г.
Введение
Многие организации в своей деятельности применяют стратегию постоянного улучшения. Для ее выполнения в части управления процессами организация должна оценивать воспроизводимость и пригодность своих ключевых процессов. В этом случае применимы методы, установленные в стандартах серии ИСО 22514. Основой успешного применения действий по непрерывному улучшению оценки показателей пригодности и воспроизводимости является постоянный анализ стабильности и источников изменчивости своих процессов.
Особенностью настоящего стандарта является то, что в нем четко определены понятия «условия воспроизводимости процесса» и «условия пригодности процесса», первичное различие которых состоит в наличии (воспроизводимость процесса) или отсутствии (пригодность процесса) подтверждения статистической стабильности процесса. Поэтому при оценке пригодности и воспроизводимости применяют два набора индексов, которые приведены в соответствующих разделах настоящего стандарта. Это необходимо, так как многие организации не учитывают их различия и, соответственно, неверно трактуют полученные индексы.
Изложение настоящего стандарта построено по принципу от общего к частному, что позволяет получить общие формулы, а также их представление в более частном виде.
В настоящем стандарте имеется много ссылок, показывающих важность понимания процессов в деятельности любой организации, будь это производственный процесс, оказываемая услуга или процесс обработки информации. В условиях конкуренции для организации важна не только цена продукции или обслуживания, но также и затраты, которые понесет покупатель при использовании продукции или услуги. Поэтому целью любой организации является непрерывное уменьшение изменчивости, а не только соответствие установленным требованиям.
Стратегия постоянного улучшения обеспечивает сокращение затрат, связанных с отказами, и повышает устойчивость развития организации в условиях конкуренции. Кроме того, снижение изменчивости процесса позволяет сократить затраты на контроль или уменьшить частоту выборочного контроля.
Оценка воспроизводимости и пригодности процесса также необходима организации для контроля воспроизводимости и пригодности процессов ее поставщиков. Для этих целей настоящий стандарт будет полезен многим организациям.
Количественная оценка изменчивости процесса позволяет сделать выводы о его пригодности и соответствии установленным требованиям. Настоящий стандарт обеспечивает необходимую основу для понимания воспроизводимости и пригодности любого процесса.
Все процессы обладают некоторой присущей им изменчивостью. Настоящий стандарт не устанавливает понятий собственной изменчивости процесса, ее возникновения и влияния на процесс. В стандарте использовано предположение, что изменчивость существует и стабильна.
Владельцы процесса должны анализировать и определять источники изменчивости своих процессов. Для идентификации этой изменчивости могут быть использованы такие методы, как составление блок-схемы и идентификация входов и выходов процесса, использование причинно-следственной диаграммы (рыбий скелет).
Для пользователя настоящего стандарта важно понимать наличие изменчивости, которая может иметь краткосрочную или долгосрочную природу, и то, что определение воспроизводимости, использующее только краткосрочную изменчивость, может значительно отличаться от определения воспроизводимости, использующего долгосрочную изменчивость.
При анализе краткосрочной изменчивости может быть выполнено исследование, использующее очень короткий срок изменений, иногда называемое анализом оборудования. Метод выполнения такого исследования не рассматривается в настоящем стандарте, однако необходимо отметить, что такие исследования важны и полезны.
Следует заметить, что индексы воспроизводимости, вычисленные в соответствии с ISO/TR 22514-4, представляют собой точечные оценки истинных значений. Поэтому рекомендуется по возможности определять и записывать доверительные интервалы индексов. В настоящем стандарте установлены необходимые для этого методы.
Применяемый в настоящем стандарте международный документ разработан техническим комитетом ИСО/ТС 69 «Применение статистических методов».
1 Область применения
В настоящем стандарте установлены наиболее применимые показатели воспроизводимости и пригодности процесса, а также методы оценки индексов воспроизводимости и пригодности в случае нормального, логнормального и других распределений наблюдаемой характеристики.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 Основополагающие термины
2.1.1 продукция (product): Результат процесса.
2.1.2 характеристика (characteristic): Отличительный признак.
1 Характеристика может быть присущей или присвоенной.
2 Характеристика может быть качественной или количественной.
3 Существуют различные классы характеристик, такие как:
— физические (например, механические, электрические, химические или биологические характеристики);
— органолептические (например, связанные с обонянием, осязанием, вкусом, зрением, слухом);
— этические (например, вежливость, честность, правдивость);
— временные (например, пунктуальность, безотказность, доступность);
— эргономические (например, физиологические характеристики или связанные с безопасностью человека);
— функциональные (например, максимальная скорость самолета).
2.1.3 характеристика качества (quality characteristic): Присущая продукции (2.1.1), процессу или системе характеристика (2.1.2), относящаяся к требованию.
1 Слово «присущая» означает свойственность чему-либо, особенно если это относится к постоянной характеристике.
2 Присвоенные характеристики продукции, процесса или системы (например, цена продукции, владелец продукции) не являются характеристиками качества этой продукции, процесса или системы.
2.1.4 граница поля допуска (specification limit): Предельное значение, установленное для характеристики (2.1.2).
2.1.5 установленное поле допуска (specified tolerance): Область между верхними и нижними границами поля допуска (2.1.4).
2.1.6 целевое значение, (target value, ): Предпочтительное или опорное значение характеристики (2.1.2), установленное в спецификации.
2.1.7 распределение характеристики (distribution ): Описание вероятностных свойств характеристики (2.1.2).
2.1.8 вид распределения (class of distributions): Группа распределений (2.1.7), имеющих общие параметры, полностью определяющие данную группу распределений.
2.1.9 модель распределения (distribution model): Конкретное распределение (2.1.7) или вид распределения (2.1.8).
2.1.10 границы опорного интервала (reference limits): Квантили распределения (2.1.7) характеристики продукции назначенного уровня.
2.1.11 опорный интервал (reference limits): Интервал, границами которого являются квантили распределения 

Вероятно, самый старый в рунете сайт о менеджменте качества
Величайшее из безобразий есть безобразие заповедовать другому делать то, чего сам не исповедуешь. (Преп. Антоний Великий)
Индексы воспроизводимости процессов
(Компания Форд Мотор, отдел трансмиссии и шасси, П. О. бокс 2097(7) Ливония, М1 48150)
Величина C p =1,0 указывает, что процесс признается «воспроизводимым», как показано на рис. 2. Вообще надо оценивать стандартное отклонение процесса в формуле (1) для получения оценки воспроизводимости процесса C p ^. Из-за выборочной вариации и ограничений измерительного оборудования, обсуждаемых ниже, C p ^=1,0 обычно не используется как минимальное приемлемое значение.
Рисунок 2. Распределение отдельных деталей для воспроизводимого процесса (Ср=1).
Рисунок 3. Индексы Ср для различных диапазонов распределения процесса
84 части на миллион
>0.1 части на миллион
Воспроизводимый процесс, в основе которого лежит стабильное нормальное распределение, теоретически дает в результате 0,27% изделий с параметрами, выходящими за пределы допусков. Значение 1,0 было выбрано для демонстрации связи C p со стандартным шестисигмовым отклонением, используемым в контрольных картах. Если процесс точно воспроизводим, то:
НГУ-нижняя граница управления;
Соотношение в формуле (2) указывает, что границы допуска, скорректированные на объем выборки, равны контрольным границам для процесса с C p =1,0.
Первоначально C p использовалось для проведения сравнений разного рода. На рис. 3 показано, как различные значения C p относятся к разбросу процесса с учетом ширины допуска. Минимальное значение C p =1,33 обычно применяется к текущему процессу (см. Джуран, Грыня и Бингхем (1979 р. 9-22 ). Оно отражает очень низкую долю брака (0,007%) и таким образом служит ориентиром для эффективной стратегии предотвращения, производства бракованных изделий. Значение C p =1,33 часто используется для оценки качества оборудования, так как долговременный статистический контроль обычно нельзя организовать во время сертификационных испытаний. Применение показателя 1,33 дает некоторую гарантию, что по крайней мере сохранится C p =1,0, если в процессе производства возникнут, как подсказывает опыт, дополнительные источники вариации. Следует заметить, что по-видимому более естественно применять традиционный показатель:
Обсуждение выборочных ситуаций
Выборочную вариацию C p ^ в (3) можно легко изучить, поскольку известно, как применить хи-квадрат распределение выборочной дисперсии (s 2 ). Бурр (1976, pp. 336-341) выводит кривую оперативной характеристики (ОХ) для проверки стандартного отклонения, используя тот факт, что (N-l)s 2 /s 2 имеет хи-квадрат распределение с (N-1) степенями свободы. По аналогии можно рассчитать кривую ОХ для проверки воспроизводимости процесса. Прежде всего следует отметить, что проверка гипотезы (s 0 >0)
эквивалентна проверке воспроизводимости процесса (c 0 >0)
При использовании критической области C p ^>с функция мощности критерия (4) получается непосредственно из хи-квадрат распределения выборочной дисперсии как:
Пользуясь формулой (5), можно вычислить кривую ОХ (C p )=1-p (C p ) и использовать ее для сравнения вариантов проверки. Кривая ОХ позволяет понять порочность практики, когда пренебрегают оценкой вариации выборки s ^ при оценивании воспроизводимости процесса. Пусть мы хотим выяснить, воспроизводим ли процесс на уровне с 0 =1,33 (то есть H 0 : C p? 1,33) при N=30 изделиям, а предел браковки (критическое значение) c=1,33. Кривая ОХ (а) на рис. 4 показывает, что ОХ (1,33)=0,40, а это значит, что вероятность ложного суждения о процессе как о невоспроизводимом (принятие гипотезы H 0 ) равна 40%. Истинная воспроизводимость процесса должна быть C p =1,6 чтобы оставалось всего 5% шансов для причисления процесса к невоспроизводимым при критическом значении С=1,33.
Рисунок 4. Кривая оперативной характеристики для плана выборки, который отбрасывает гипотезу о воспроизводимости процесса, если Ср
Исходя из формулы (5) a и b риски будут:
Решая относительно C p (высокая)/C p (низкая) и с получим:
Подход с использованием интервала допуска
Верхний и нижний показатели воспроизводимости
Рассмотрим ситуацию с односторонним допуском, когда задан только один предел. На рис. 5 показано распределение процесса относительно верхней границы допуска. Соотношение фактического и допустимого размаха точно так же, как и в (1), дает новый показатель CPU:
Индекс CPU был разработан в Японии и применяется во многих японских компаниях. Для нижней границы допуска совершенно аналогично формуле (7) имеем:
Рисунок 5. Соотношение параметров CPU.
Оценки CPU и CPL обозначаются CPU и CPL и получаются при замене m и ? на ` х и s соответственно. Индексы CPU (верхний C p ) и CPL (нижний C p ) связаны с C p через:
и применяются для измерения воспроизводимости процесса при наличии только одной границы допуска. Само собой разумеется, что в случае с одной границей допуска CPU=1,0 означает половину бракованных деталей (0,136%) по сравнению с тем, что дает C p =1,0 в случае с двусторонним допуском.
Рисунок 6. Соотношение параметров Срк.
НОМИНАЛЫ (ЦЕЛЕВЫЕ ЗНАЧЕНИЯ)
Рисунок 7. Воспроизводимость процесса в случае использования целевых значений (номиналов).
Есть множество способов распространения введенных показателей воспроизводимости на случай целевого значения (номинала). Следующее расширение использует аналогию между фактическим и допустимым разбросами процесса, которая показана на рис. 1. Показатель потенциала процесса связывает фактический разброс процесса с допустимым. Из рис. 8 для ближайшего к ВГД значения Т имеем:
Рисунок 8. Соотношение параметров Ср при использовании целевых значений.
Такую же аналогию можно применить и к показателю k. Из рис. 9 для ближайшего к ВГД значения T, имеем:
Рисунок 9. Соотношение параметров К при использовании целевых значений.
Простой пример иллюстрирует применение этих индексов. Предположим, что ВГД=18, НГД=10, T=16, s =0,67. Обратите внимание, что из формулы (11) C p =1,0. На рис. 10 представлены индексы воспроизводимости для выбранных значе ний среднего.
Рисунок 10. Индексы воспроизводимости процесса при целевом значении T=16.
Опыт показал, что в использовании C p и C pk на традиционной основе заложены потенциальные трудности. Эти недостатки в общем возникают из-за пользователей, которые не имеют полного представления о статистических принципах, а не из-за проблем, присущих самим индексам. Некоторые из этих недостатков описываются ниже.