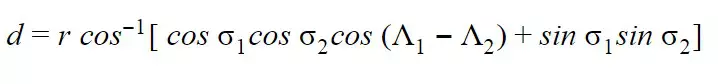Что обозначает прямая линия на географической карте
Посмотрите на схему. Точка O — центр Земли. Точки A и B находятся на поверхности Земли.
Круг, полученный при пересечении шара плоскостью, проходящей через его центр, называется больши́м. На схеме голубым цветом показан большой круг, проходящий также через наши точки A и B.
Эти наши точки делят окружность, ограничивающую большой круг, на две дуги — бо́льшую и меньшую.
Так вот, меньшая дуга большого круга, проходящего через точки A и B, и будет ОРТОДРОМИЕЙ, кратчайшим расстоянием между двумя этими точками. На схеме ортодромия показана тёмно-зелёной линией
Теперь посмотрите вот на эту картинку. Та же предыдущая схема, только с нанесёнными меридианами.
Посмотрите: наша ортодромия пересекает меридианы (тонкие тёмно-синие линии) под разными углами. Запомним этот факт и пойдём дальше.
Если же у вас под рукой есть глобус, можете сами построить произвольный большой круг с помощью ниточки и воочию убедиться, что он будет пересекать меридианы под разными углами.
А дальше мы приходим уже к Яндекс.Картам.
Яндекс.Карта составлена в равноугольной цилиндрической проекции Меркатора. То есть, и меридианы, и параллели на этой карте являются отрезками прямых, пересекающихся под прямым углом:
(4)
Теперь давайте рассуждать таким образом. Меридианы на этой проекции являются параллельными отрезками прямых. Следовательно, любая прямая линия, начерченная на этой карте, пересекала бы меридианы под одним и тем же углом (см. зелёную линию на самой первой картинке). Но ортодромия пересекает меридианы под разными углами. А линия, пересекающая параллельные прямые под разными углами, прямой быть ну никак не может. Она будет как раз-таки кривой.
Кстати, линия, пересекающая меридианы под одним и тем же углом, называется локсодромией. На цилиндрических проекциях локсодромии как раз-таки прямые.
А бывают ли, всё-таки, ортодромии, которые отобразятся на Яндекс.Карте отрезками прямых? Бывают-бывают.
Например, есть одна-единственная параллель, ограничивающая большой круг. Это экватор.
Судите сами: во-первых, это линия, ограничивающая большой круг. Во-вторых, это параллель. А параллели в цилиндрической проекции являются параллельными прямыми линиями, пересекающими меридианы под одним и тем же (прямым, ага) углом. Следовательно, дуги большого круга (в том числе и ортодромии) на экваторе будут прямыми.
1 Ну, на самом деле, не шар. Всё намного сложнее и интереснее. Я про фигуру Земли потом расскажу, а пока пусть Земля будет шаром.
Географическая карта и план местности
Урок 2. Подготовка к ЕГЭ по географии
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Географическая карта и план местности»
Сегодня на уроке вы узнаете, что такое географическая карта, какие бывают виды карт, что такое план местности и в чём его назначение, разберётесь, в чём отличия карты от плана. Приступим.
Что такое географическая карта?
Карта – это «язык» географии. Без неё невозможно было бы существование и самой науки.
Историческая справка. Первая географическая карта появилась ещё в Древней Греции.
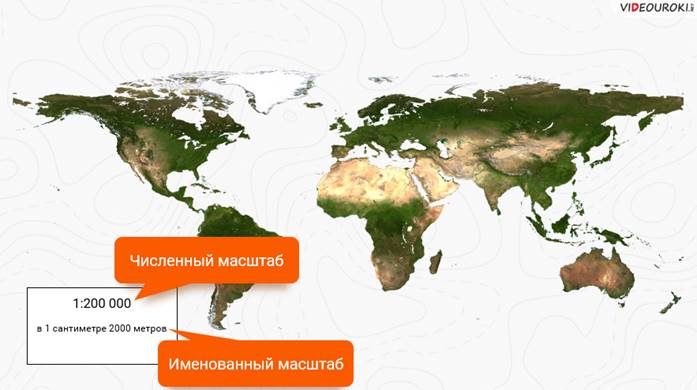
Масштаб записывают в следующем виде: 1:200 000. Это означает, что 1 сантиметр на карте соответствует 2000 метрам на местности. Первый вид масштаба называют «численный», а второй – «именованный». Чтобы перевести численный масштаб в именованный, нужно число в численном масштабе поделить на 100, так как эта величина указана в сантиметрах. Как известно, в одном метре 100 см. Тогда нужно 200 000 поделить на 100. Получим 2000 м. Значит, 1 см на карте соответствует 2000 м на местности.
По масштабу географические карты делят:
на крупномасштабные, построенные в масштабе 1: 200 000 и крупнее (в 1 см 2 км и крупнее);
среднемасштабные, построенные в масштабе мельче (чем в 1 см 2 км до в 1 см 10 км включительно) 1: 200 000 до 1: 1 000 000 включительно;
мелкомасштабные, построенные в масштабе мельче 1: 1 000 000 (чем в 1 см 10 км).
Вы помните, что Земля имеет шарообразную форму, т. е. поверхность её является выпуклой.
Как же на бумаге можно отобразить круглую Землю?
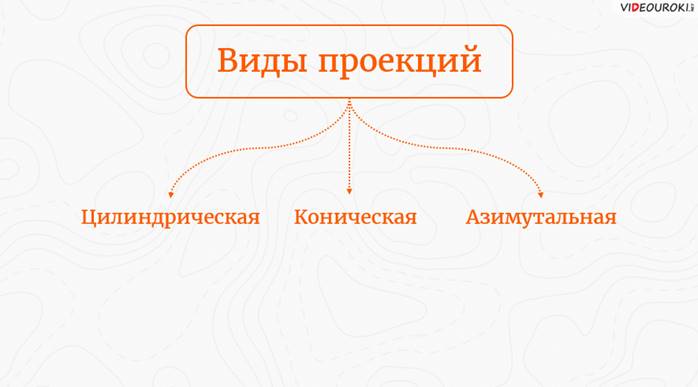
Для переноса выпуклой поверхности на плоскость используют картографические проекции.
Перейдём к этапам создания той или иной проекции.
Вначале путём проектирования на вспомогательную поверхность переносят линии меридианов и параллелей, совокупность которых составляет картографическую сетку. Затем на ней строят картографическое изображение. Вид проекций подбирается исходя из размера изображаемой территории и цели картирования.
Глобус оборачиваем бумажным цилиндром так, чтобы он касался линии экватора и проектируем на внутреннюю поверхность цилиндра градусную сеть. Развернув цилиндр, мы увидим, что меридианы и параллели образуют сеть прямоугольников. Такая проекция удобна для изображения поверхности всего земного шара, но при этом появляются большие искажения. Все параллели цилиндрической поверхности равны по длине, на глобусе их длина уменьшается к полюсам. Меридианы также равны между собой, но имеют вид прямых параллельных линий, а на глобусе они сходятся у полюсов.
Градусную сеть глобуса проецируем на две плоскости, касающиеся глобуса в противоположных точках экватора, и получаем карту полушарий. В такой проекции параллели изображаются концентрическими окружностями, а меридианы – их радиусами, углы между которыми равны соответствующим разностям долгот. Азимутальные проекции применяются для карт полярных стран, для Арктики и Антарктиды.
Ещё один немаловажный момент: поверхность Земли неровная (из-за рельефа). Чтобы показать это на карте, используют специальные отметки высот областей материков и глубин морей и океанов. Кроме того, разные высоты и глубины обозначают разными оттенками цвета.
Методы масштабирования и картографических проекций используют математические расчёты, поэтому-то карту и называют математической моделью земной поверхности.
Перейдём к вопросу классификации географических карт.
По обхвату территории различают карты мира, полушарий, материков и их крупных частей, океанов и морей, государств, областей, районов.
По содержанию географические карты делятся на два вида: общегеографические и тематические. Общегеографические карты изображают рельеф территорий, климат, политическое деление, растительно-почвенный покров.
Тематические карты показывают динамику и взаимосвязи населения, экономики, природных явлений. Среди них различают физико-географические карты (геологические, климатические, почвенные) и социально-экономические карты (политические, политико-административные, карты населения, экономические и др.)
По назначению выделяют карты многоцелевого назначения (топографические карты), научно-справочные, учебные, туристические, навигационные, военные и другие.
Разные карты объединяют в атласы.
Разрабатывая ту или иную географическую карту, невозможно на ней отобразить все объекты. Поэтому на картах изображают только главные, самые важные объекты, то есть проводят генерализацию.
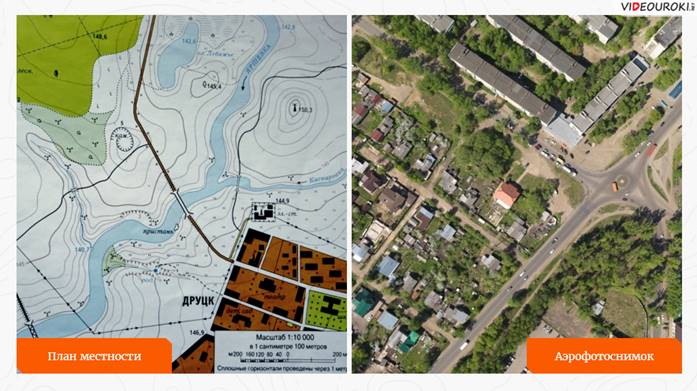
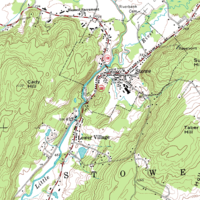
Давайте разберёмся, что же такое план местности.
План местности — чертёж небольшого (порядка 0,5 км) участка местности в крупном масштабе с помощью условных знаков. Он напоминает вид сверху и похож на аэрофотоснимок, но объекты местности показаны условными знаками и сопровождаются надписями. Рельеф на планах изображается горизонталями. Это линии на плане или карте, соединяющие точки земной поверхности с одинаковой высотой.
Обратите внимание: если склон крутой, горизонтали на плане будут расположены близко друг к другу, если же пологий — далеко. Маленькие чёрточки, проведённые перпендикулярно к горизонталям (бергштрихи), показывают, в каком направлении склон понижается.
Из-за небольших размеров изображаемой территории на плане нет необходимости учитывать кривизну земной поверхности. Чем меньше территории, тем меньше искажения, поэтому их можно не учитывать и, следовательно, не отображать.
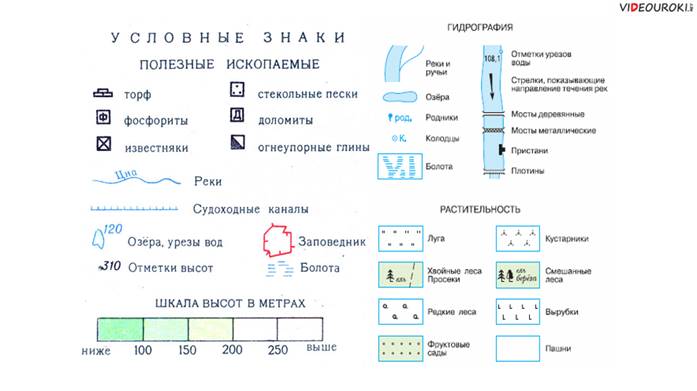
Чтобы работать с планом местности, нужно уметь его читать, т. е. знать, что обозначают условные знаки. Их много, и они похожи на сами объекты. Выделяют площадные, внемасштабные и линейные условные знаки.
Площадные условные знаки отображают объекты местности, которые занимают определённую площадь. Например, лес, фруктовый сад, пашня.
Внемасштабные условные знаки – это знаки, которые отображают одиночный объект местности, который на плане нельзя отобразить в масштабе. Например, отдельно стоящее озеро, родник, овраг.
Линейные условные знаки отображают те объекты местности, которые имеют вид линий. Например, дорога, река, просека. Для простоты вид условных знаков схож с теми объектами, которые они отображают, к тому же каждому условному знаку соответствует определённый цвет. Например, лес отображают зелёным цветом, а водоёмы и реки – голубым.
Обратите внимание на то, что все условные знаки на плане местности изображаются равными по размерам, высоте, форме и цвету.
На плане объекты местности невозможно показать в натуральную величину, так как они попросту не вместятся на лист бумаги.
При составлении плана местности обязательно используется масштаб. В этом, а также в использовании условных обозначений заключается сходство плана и географической карты. План так же, как и карта, сориентирован по сторонам горизонта. Однако стороны горизонта на карте и плане обозначаются по-разному: на карте для этой цели служит сеть параллелей и меридианов, а на плане направление сторон горизонта указывают стрелкой. Если на географической карте северное направление всегда вверху листа, то расположение изображения участка местности на плане может быть произвольным (т. е. северное направление не привязано к верху плана). Масштаб плана и карты всегда различается. На плане изображают небольшие по площади территории, поэтому его масштаб всегда крупный, что позволяет более точно, в мелких деталях, изобразить местность. Из этой особенности плана вытекает различие в наборе условных знаков на плане и карте.
Причины всех указанных отличий в том, что карта и план, выполняя одну и ту же функцию, служат разным целям. Назначение плана местности — отобразить точное взаиморасположение всех объектов в пределах территории.
Важно уметь пользоваться планом местности. Так, например, находясь в незнакомом городе, но имея его план, можно найти нужную вам улицу или дом, магазин, музей и сквер. Строители, пользуясь планом местности, решают, где лучше проложить новую дорогу, построить новые дома, а где этого делать не нужно.
Подведём итоги урока.
План и карта – это пособия для изучения географии, второй учебник. Они имеют огромное значение для жизни человека. Только умея «читать» план и карту, можно получить глубокие и прочные знания по географии, которыми вы сможете воспользоваться в любой жизненной ситуации.
Основные различия плана местности и географической карты мы представим в виде таблицы. Из неё вы видите, что:
При составлении плана используют более крупный масштаб.
План охватывает меньшие по площади территории.
На плане, в отличие от карты, не учитывается кривизна земной поверхности.
На плане направление сторон горизонта указывают стрелкой, на карте они обозначены градусной сетью.
На плане и карте используются разные системы условных обозначений.
Нет, прямая линия не всегда является самым коротким расстоянием между двумя точками. Наименьшее расстояние между двумя точками зависит от геометрии объекта/поверхности. Для плоских поверхностей линия действительно является кратчайшим расстоянием, но для сферических поверхностей, таких как Земля, расстояния по большому кругу на самом деле представляют собой самое короткое расстояние.
Как оказалось, это утверждение лишь отчасти правдиво. Самое короткое расстояние между двумя точками на самом деле зависит от геометрии рассматриваемого объекта.
Большое расстояние круга
Большое расстояние круга не новая концепция; на самом деле, многие из вас уже видели это в действии.
Люди, которые путешествовали по воздуху или только проверяли маршруты полета, вероятно, заметили, что рейсы не следуют прямым путем, а вместо этого берут изогнутый маршрут к месту назначения. Изогнутые маршруты не используются для того, чтобы выкопать более глубокую яму в карманах пассажиров, а используются потому, что на самом деле они являются самым коротким расстоянием между любыми двумя заданными точками на нашей планете.
Эти изогнутые маршруты часто сбивают с толку, так как маршруты очерчены на плоской двухмерной карте, где прямая линия может показаться наименьшим расстоянием. Однако ни одна двумерная карта Земли не является точной.
Чтобы дать вам понять суть, наша любимая Земля является трехмерным пространством и лучше всего представлена с помощью модели глобуса. Однако, когда пытаешься сравнять сферу с прямоугольной формой, как это делают большинство карт, на первый план выходит вековая дилемма искажений. Большинство прямоугольных карт торгуют формами страны, размерами, промежуточными расстояниями и даже легитимной информацией для удобства понимания.
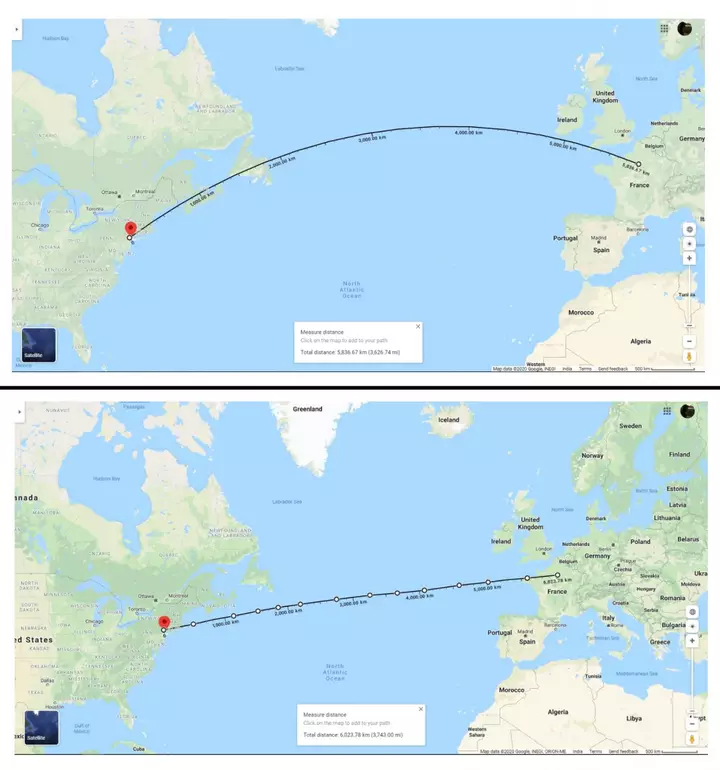
Представьте, что вы хотите улететь из кишащих крысами глубин Нью-Йорка в город любви, Париж. На глобусе кратчайшее расстояние между двумя городами было бы дугой примерно 3630 миль, но та же самая дуга, когда она проецируется на 2D-карту, превращается в прямую линию, измеряющую приблизительно 3750 миль.
Чтобы убедиться в этом самим, откройте Google Maps на соседней вкладке и найдите Нью-Йорк. Найдя его, щелкните правой кнопкой мыши на именном теге и выберите «измерить расстояние». Затем уменьшите масштаб или прокрутите немного вправо, чтобы найти Париж, и нажмите на него. Следующее расстояние будет представлять собой кривую, представляющую собой кратчайшее расстояние между двумя городами. Нажмите в любом месте на этой кривой, чтобы сделать ключевую фигуру, и перетащите её немного на юг, чтобы преобразовать кривую в прямую линию. Вы можете использовать несколько ключевых кадров, чтобы составить прямую линию между двумя точками. После этого сравните размеры кривой и прямой линии (и приготовьтесь к тому, что ваша реальность будет разрушена!).
Разница между двумя числами (3,750 – 3,630 = 120 миль) может показаться несущественной, но, учитывая тот факт, что Boeing 747 потребляет в среднем 5 галлонов топлива на милю полета, самолет потребует дополнительных (5 галлонов/км × 120 миль =) 600 галлонов (2250 литров), чтобы пройти дополнительное расстояние, что является большим делом и добавит к стоимости билетов на самолет.
Расстояние большого круга в математических терминах
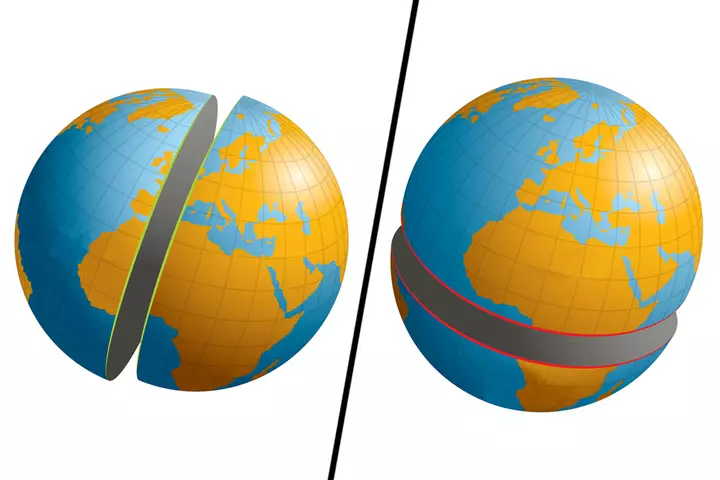
Представьте себе (или просто посмотрите на рисунок ниже), разрезая землю вдоль экватора или полюсов. Результирующие полушария в обоих случаях будут равны, и грани этих полушарий будут иметь тот же диаметр и центр, что и сама сфера (Земля).
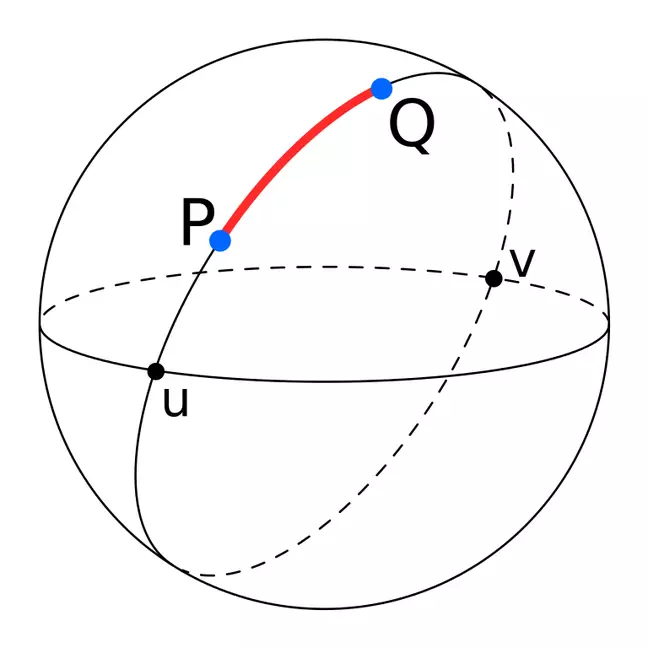
Для любых двух не диаметральных точек (положений) на сфере (Земле) существует только один уникальный большой круг, тогда как для диаметральных точек на сфере можно нарисовать бесконечное число больших кругов. Эти точки делят окружность на две дуги; меньшая дуга представляет собой истинное кратчайшее расстояние между двумя точками и называется расстоянием большого круга.
На приведенном ниже изображении точки P и Q являются двумя не диаметральными точками, а дуга PQ представляет собой кратчайшее расстояние между ними (расстояние большого круга). Точки u и v, с другой стороны, известны как противоположные или диаметрально противоположные точки и разделяют большой круг на две идентичные дуги.
Вычисление расстояния большого круга между любыми двумя точками на поверхности сферы требует использования сферической тригонометрии, и хотя мы, возможно, не были знакомы с существованием больших расстояний круга еще в наши школьные годы, всеобщая ненависть к синусам и косинусам хорошо известна.
Как уже говорилось ранее, большие круги находят свое основное применение в дальних путешествиях, в частности в воздушной и морской навигации. Искривленный характер больших окружных расстояний, дополненный вращением нашей планеты, заставляет пилотов и моряков постоянно корректировать свой курс. Поэтому большое расстояние по окружности разбивается на «линии Румба», которые представляют собой постоянное направление.
Сказав все это, даже большие расстояния по кругу не представляют собой истинное кратчайшее расстояние между двумя заданными местоположениями. Расстояния большого круга рассчитываются исходя из предположения, что Земля является идеальной сферой, но планета представляет собой более плоскую сферу с различными значениями радиуса в направлении экватора и полюсов. Значения большого круга, таким образом, имеют допуск около ± 5%.
Тем не менее большие расстояния по окружности сыграли огромную роль в дальних поездках за последние несколько лет и будут продолжать делать это, экономя топливо авиакомпаний и экономя деньги путешественников!
Что такое параллели и меридианы в географии и для чего они нужны
В географической науке есть такие интересные понятия, как параллели и меридианы — что же это такое? Параллели и меридианы — наши помощники в определении местоположения в мире любого объекта. Это условные линии, пересекающие модель Земли (на глобусе или карте) в горизонтальном и вертикальном направлении, которых в природе на самом деле не существует. Вместе они образуют градусную сеть, пересекающую всю поверхность земного шара. Это позволяет максимально точно определить положение любой точки на планете.
Основные понятия
Широта и долгота и есть те самые координаты параллелей и меридианов. Таким образом, когда определенная широта и долгота пересекаются, появляется точка, имеющая уникальные координаты, которые измеряются в градусах. Также широту и долготу можно измерять километрами.
Важно! Градусное значение широты и долготы для одной линии одинаково.
Условно разделяя Земной шар на отдельные сегменты, можно заметить различия и закономерности в признаках.
Важно! Сколько можно провести линий? Параллелей и меридианов можно проводить бесконечное множество. От частоты их проведения будет зависеть точность измерений.

Параллели
По горизонтали через всю поверхность проходят параллельные друг другу окружности, которые имеют разный диаметр и не имеют ни одной общей точки. Отсюда и название линий — параллели. У полюсов располагаются самые короткие по диаметру окружности. А самая большая длина — у линии, проходящей в самом центре, которая имеет уникальное название — экватор.
Важно! Экватор — это самая длинная параллель (около 40000 км), которая равноудалена от Северного и Южного полюсов. Именно здесь проходит граница, разделяющая полушария на Северное и Южное.
Параллели — северные и южные широты, обычно на картах или глобусе подписаны как “с.ш.” и “ю.ш”.
Меридианы
Существуют линии, которые движутся в вертикальном направлении с севера на юг — меридианы. Эти линии представляют собой дуги одинаковой длины (около 20000 км), соединяющие северный полюс с южным. В конечном счете все они сходятся в крайних точках полюсов Земли.

Отсчет начинается с нулевого меридиана — пояса Гринвича.
Меридианы — западные и восточные долготы обозначаются как “з.д.” и “в.д.”.
Важно! Место в Тихом океане, где встречаются западная и восточная долгота, называется линией перемены дат. Она имеет меридиональное направление. Пересекая эту линию, мы автоматически попадаем в следующий день, совершая скачок во времени ровно на 24 часа.
Наименьшее расстояние от одного меридиана до другого равное 1° равняется 111,11 км, а ближе к полюсам стремится к 0°. А самым распространенным интервалом между меридианами являются 15° равные 1 часу времени.
Важно! Наша планета Земля совершает 1 полный оборот вокруг своей оси за одни земные сутки, равные 24 часам. Исходя из этого, планета делится на 24 зоны, называемыми часовыми поясами.
Географические координаты России
Какой город в нашей стране является точкой отсчета остальных часовых поясов России? — Конечно, Москва. С меридиана, на котором находится столица нашего государства начинается отсчет времени в других городах.
Важно! Наша страна обладает обширными территориями и простирается почти на 12 часовых поясов. Однако, исходя из административного деления Российской Федерации, Россия имеет 11 часовых поясов.

Наши помощники — глобусы и карты
Как уже отмечалось ранее, в природе таких линий, как параллели и меридианы, вы не увидите. Однако на любой карте или глобусе они станут вашими верными помощниками и ориентирами.
Для того чтобы было удобно изучать наш мир, ученые создали несколько вариантов представления нашей планеты в миниатюре. На плоскости — это различные карты, а объемной моделью является глобус. Глобус характеризуется наибольшей точностью, чем карты, так как имеет осевой наклон, и на объемной модели искажение не такое сильное.
С помощью градусной сетки можно легко посчитать точные координаты конкретного объекта, который вас интересует, и даже вычислить расстояния от одной точки до другой, учитывая масштаб карты.
Для еще большей точности можно разделить градус на минуты, и даже на секунды.
Таким образом, сегодня вы расширили свои горизонты и узнали, что с помощью волшебных линий на карте или глобусе можете определить местоположение любого объекта на планете. Важно понимать, что изображение градусной сетки на плоскости (карта) и в объемном виде (глобус) внешне будут значительно отличаться. На карте будут зрительные искажения, так как на плоскую поверхность перенесли модель объемной фигуры, но общепринятые значения от этого не меняются. Увидеть наглядные примеры расчетов координат и построение сетки широты и долготы на карте и глобусе вам поможет нижепредложенное видео.
Географическая карта
Имеющие общий замысел карты могут объединяться в атлас.
Общие определения карты пространства (местности):
Карта — это построенное в картографической проекции, уменьшенное, обобщенное изображение поверхности Земли, другого небесного тела или внеземного пространства, показывающее расположенные на ней объекты или явления в определенной системе условных знаков.
Карта — математически определённая образно-знаковая модель действительности.
Содержание
Классификация
Географические карты подразделяются на следующие категории:
По территориальному охвату
По масштабу
Отличные по масштабу карты имеют разную точность и детальность изображения, степень генерализации и разное назначение.
По назначению
По содержанию
Создание карт
Созданием картографических произведений занимается раздел картографии картоведение. Создание карт выполняется с помощью картографических проекций — способа перехода от реальной, геометрически сложной земной поверхности к плоскости карты. Для этого сначала переходят к математически правильной фигурe эллипсоида или пули, а затем проектируют изображение на плоскость с помощью математических зависимостей. При этом используют различные вспомогательные поверхности: цилиндр, конус, плоскость.
Искажения карт
На любых географических картах существуют искажения длин, углов, форм и площадей. Эти искажения разных видов, а их величина зависит от вида проекции, масштаба карты и охвата проектируемой территории. Обнаружить на карте искажения длин вдоль меридианов можно, сравнив отрезки меридианов между двумя соседними параллелями — если они находятся на одном уровне, то искажений длины нет. Об искажении расстояний на параллелях свидетельствует соотношение длин отрезков экватора и параллели 60°-й широты между соседними меридианами. Если искажения отсутствуют, то отрезок экватора ровно в два раза больше, чем отрезок 60°-й параллели.
О характерном для большинства карт искажении углов можно сделать вывод в том случае, когда параллели и меридианы не образуют между собой прямых углов.
Различить искажения формы можно сравнив длину и ширину какого-либо географического объекта на карте и глобусе — если соотношения форм пропорциональны, то искажения по данному критерию нет. Ещё проще различить искажения формы можно сравнив ячейки сетки на одной широте: если они одинаковы, то это свидетельствует об отсутствии искажений формы на данной географической карте.
В зависимости от назначения карт, для них подбирают такие проекции, на которых один из видов искажений может отсутствовать, или быть пренебрежимо малым. По характеру искажений картографические проекции делятся на