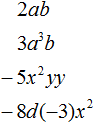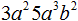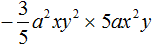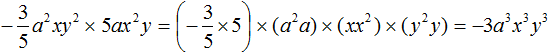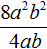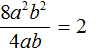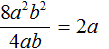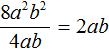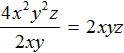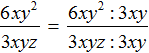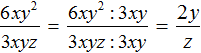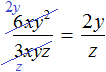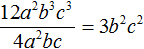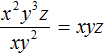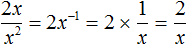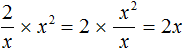Что нужно сделать чтобы возвести одночлен в степень

Взведение одночлена в степень

Возведение одночлена в степень проводится по правилам возведения в степень произведения и степени.

Чтобы возвести одночлен в степень, надо возвести в эту степень каждый множитель одночлена и полученные результаты перемножить.

Возвести в степень одночлен:

Чтобы возвести одночлен в четвертую степень, надо возвести в 4-ю степень каждый из входящих в него множителей. При возведении чисел в степень удобно пользоваться таблицей степеней.

]При возведении в степень обыкновенной дроби возводят в степень и числитель, и знаменатель.

При возвести в степень смешанного числа сначала его нужно перевести в неправильную дробь, затем возвести в степень отдельно числитель, отдельно — знаменатель.

Последний этап — из неправильной дроби следует выделить целую часть.

Если коэффициент одночлена является отрицательным числом, начинать возведение одночлена в степень следует с определения знака результата.

При возведении отрицательного числа в четную степень получается положительное число, в нечетную — отрицательное.

Здесь отрицательное число возводим в третью, то есть нечетную, степень. В результате получаем отрицательное число.

Отрицательное число возводим во вторую, то есть четную, степень. В результате получаем положительное число. Смешанное число переводим в неправильную дробь и возводим в квадрат и её числитель, и знаменатель. Из полученной неправильной дроби выделяем целую часть.

Источник

Возведение одночлена в степень, правило, примеры.

Ранее мы определили умножение одночлена на одночлен, это позволяет ввести еще одно действие – возведение одночлена в степень. Ниже мы получим правило возведения одночлена в степень с натуральным показателем, и рассмотрим решения примеров, чтобы разобрать все нюансы.

Навигация по странице.

Из приведенных рассуждений, во-первых, отчетливо видны все действия, из которых состоит процесс возведения одночлена в степень. Соберем их вместе в виде правила возведения одночлена в степень.

Чтобы возвести одночлен в степень, нужно

Во-вторых, из разобранного выше примера видно, что результатом возведения одночлена в степень является новый одночлен. Здесь отметим, что если исходный одночлен записан в стандартном виде, то после его возведения в степень получится одночлен стандартного вида. Если же исходный одночлен дан в виде, отличном от стандартного, то целесообразно этот одночлен привести к стандартному виду перед возведением в степень. Если этого не сделать, то к стандартному виду придется приводить одночлен, полученный после применения записанного выше правила. Мы еще вернемся к этому моменту в следующем пункте.

Примеры

Пришло время решить несколько примеров возведения одночленов в степень. Это поможет отработать применение правила из предыдущего пункта. Начнем с простеньких примеров.

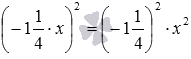
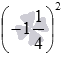
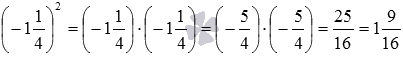
Переходим дальше. Сначала выполняем такой переход: . В последнем выражении осталось степень заменить ее значением. Так как , то .

Кратко возведение одночлена в степень для этого случая выглядит так: .

В следующем примере убедимся, что в результате возведения в степень одночлена в виде, отличном от стандартного, и соответствующего ему одночлена в стандартном виде, получаются тождественно равные одночлены.

Выполните возведение одночлена 2·x 3 ·5·x в квадрат.

Источник

Одночлены

Определения и примеры

Приведём ещё примеры одночленов:

Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 5 2 является одночленом.

Приведение одночлена к стандартному виду

Рассмотрим следующий одночлен:

Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.

Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.

Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Итак, приведём одночлен 3a 2 5a 3 b 2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:

Мы привели одночлен 3a 2 5a 3 b 2 к стандартному виду. В результате получили одночлен 15a 5 b 2

Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.

Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc

Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.

Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.

Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.

Пример 1. Привести одночлен 5xx3ya 2 к стандартному виду

Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:

Пример 2. Привести одночлен 2m 3 n × 0,4mn к стандартному виду

Перемножим числа, переменные и степени по отдельности.

Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m 3 × m и n × n

Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:

Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.

Сложение и вычитание одночленов

Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.

Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.

Пример 1. Сложить одночлены 6a 2 b и 2a 2 b

Сложим коэффициенты 6 и 2, а буквенную часть 6a 2 b оставим без изменений

Пример 2. Вычесть из одночлена 5a 2 b 3 одночлен 2a 2 b 3

Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:

Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:

Умножение одночленов

Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 1. Перемножить одночлены 5x и 8y

Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:

Пример 2. Перемножить одночлены 5x 2 y 3 и 7x 3 y 2 c

Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:

Пример 3. Перемножить одночлены −5a 2 bc и 2a 2 b 4

Пример 4. Перемножить одночлены x 2 y 5 и (−6xy 2 )

Пример 5. Найти значение выражения

Деление одночленов

Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.

Например, разделим одночлен 8a 2 b 2 на одночлен 4ab. Запишем это деление в виде дроби:

Первый одночлен 8a 2 b 2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.

Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.

Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.

В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:

Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:

Пример 2. Разделить одночлен 12a 2 b 3 c 3 на одночлен 4a 2 bc

Пример 3. Разделить одночлен x 2 y 3 z на одночлен xy 2

Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.

и такое частное при перемножении с делителем x 2 будет давать в результате делимое 2x

Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное 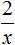целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.

Возведение одночлена в степень

Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.

Пример 1. Возвести одночлен xy во вторую степень.

Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена

Пример 2. Возвести одночлен −5a 3 b во вторую степень.

Пример 3. Возвести одночлен − a 2 bc 3 в пятую степень.

В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:

Пример 4. Представить одночлен 4x 2 в виде одночлена, возведённого в квадрат.

Пример 5. Представить одночлен 121a 6 в виде одночлена, возведённого в квадрат.

Таким образом, если произведение 11a 3 возвести во вторую степень, то получится 121a 6

(11a 3 ) 2 = 11 2 × (a 3 ) 2 = 121a 6

Разложение одночлена на множители

Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.

Пример 1. Разложить одночлен 3a 3 b 2 на множители

Данный одночлен можно разложить на множители 3, a, a, a, b, b

Либо степень b 2 можно не раскладывать на множители b и b

В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.

Пример 2. Разложить одночлен 10a 2 b 3 c 4 на множители.

Источник

как возвести одночелен в степень

Кратно: Запомните!
При возведении в степень одночлена в степень возводится числовой коэффициент и каждый буквенный множитель.

Длинно: Возьмем одночлен стандартного вида, например, 2·x·y5, и возведем его, к примеру, в третью степень. Поставленной задаче отвечает выражение (2·x·y5)3, представляющее собой произведение трех множителей 2, x и y5 в третьей степени. Можно провести тождественное преобразование записанного выражения, причем сразу напрашивается применение свойств степени. Сначала используем свойство степени произведения: (2·x·y5)3=23·x3·(y5)3. Теперь, обратившись к свойству степени в степени, (y5)3 заменяем на y15, и получаем 23·x3·(y5)3=23·x3·y15. Еще можно выполнить возведение в степень числа 2. Так как 23=8, то в итоге приходим к выражению 8·x3·y15. Очевидно, оно представляет собой одночлен стандартного вида.

Из приведенных рассуждений, во-первых, отчетливо видны все действия, из которых состоит процесс возведения одночлена в степень. Соберем их вместе в виде правила возведения одночлена в степень.

Чтобы возвести одночлен в степень, нужно

записать соответствующее выражение;
применить свойство возведения произведения в степень;
применить свойство возведения степени в степень и вычислить степени чисел.
Во-вторых, из разобранного выше примера видно, что результатом возведения одночлена в степень является новый одночлен. Здесь отметим, что если исходный одночлен записан в стандартном виде, то после его возведения в степень получится одночлен стандартного вида. Если же исходный одночлен дан в виде, отличном от стандартного, то целесообразно этот одночлен привести к стандартному виду перед возведением в степень. Если этого не сделать, то к стандартному виду придется приводить одночлен, полученный после применения записанного выше правила. Мы еще вернемся к этому моменту в следующем пункте.

РЕШАТЬ ТЕБЕ, за тебя решать не кто не будет (внимательно читай учебник, не понимаешь спроси у учителя, ну или как я зубри)!

Источник

Алгебра

План урока:

Определение степени с натуральным показателем

Периодически в математике приходится умножать число на само себя несколько раз. Пусть нам надо записать произведение десяти множителей, каждый из которых равен 2. Эта запись будет выглядеть так:

Однако существует и более компактная и удобная запись:

Говорят, что число 2 возвели в десятую степень. В данном случае двойка – это основание степени, а 10 – показатель степени:

Если показатель равен единице, то в произведении должен быть только один множитель, а потому само число не меняется:

Теперь сформулируем определение степени числа с натуральным показателем:

Важно понимать, что такое определение может использоваться только в том случае, если n – натуральное число. В старших классах будут рассматриваться примеры с дробными и отрицательными показателями, однако в таких случаях потребуются и более сложные определения этого понятия.

Отметим, что основание может быть любым числом – целым, дробным, положительным, отрицательным.

Рассмотрим несколько простейших заданий.

3 5 = 3*3*3*3*3 = 9*3*3*3 = 27*3*3 = 81*3 = 243

Обратите внимание, что при возведении отрицательного числа можно получить как отрицательное, так и положительное число. Здесь всё зависит от значения показателя. Если он четный, то получится положительное число, а если нечетный, то отрицательное.

Число 106 – четное, поэтому при вычислении (–1,365) 106 должно получиться положительное число:

Число 75 – нечетное, поэтому (– 2,512) 75 – это отрицательное число:

Очевидно, что, сколько бы мы не умножали ноль на самого себя, в результате всегда будет получаться снова 0. Поэтому при любом натуральном значении n выражение 0 n равно нулю.

Исторически сложилось, что для некоторых степеней в математике есть особое название. Квадратом числа называют его произведение на само себя. Например, квадрат шести (ещё говорят «шесть в квадрате») равен 36:

Кубом числа называют его третью степень. Так, куб пяти (ещё говорят «пять в кубе») равен 125:

5 3 = 5*5*5 = 25*5 = 125

Пример. Найдите сумму квадратов чисел (натуральных) от 1 до 5.

1 2 +2 2 +3 2 +4 2 +5 2 = 1+4+9+16+25 = 55

4 2 = 1 + 3 + 5 + 7 = 16

Попытайтесь привести доказательство этого факта. Если не получается, то просто посмотрите на следующую картинку:

Количество клеточек под каждым числом соответствует его квадрату. Видно, что для получения каждого следующего квадрата нужно добавить к предыдущему нечетное количество клеточек (выделены зеленым цветом), чтобы «достроить» его до «полного» квадрата.

Важно отметить, что в арифметических выражениях операция возведения в степень выполняется до умножения и сложения. Рассмотрим пример. Пусть надо вычислить значение выражения:

Поставим последовательность выполнения операций:

Выполним арифметические операции:

Обратите внимание, что самый первый минус в выражении относится не к пятерке, которую возводят в квадрат, а ко всему квадрату. То есть здесь сначала надо возвести 5 в квадрат, а потом изменить знак выражения

Если бы в этом примере была запись

то тогда в первом действии мы получили бы

А в четвертом выполняли бы сложение

То есть, если необходимо возвести в степень отрицательное число, то его следует записать в скобках:

Сравнение степеней

Можно заметить несколько очевидных правил, которые помогают сравнивать степени положительных чисел, не вычисляя напрямую их значения.

Правило 1. Каждая следующая степень числа, большего единицы, больше предыдущей:

Правило 2. Каждая следующая степень положительного числа, меньшего единицы, меньше предыдущей:

Правило 3. Все степени единицы равны друг другу:

1 1 = 1 2 =1 3 =1 4 =1 5 =1 6 …

Правило 4. Если две степени имеют одинаковый показатель, но различающееся основание (положительное), то больше та, у которой больше основание:

Решение: Сравнить напрямую эти числа друг с другом не получится, так как у них отличаются и показатель, и основание. Однако оба эти выражения можно сравнить с другим числом 0,99 1000 :

На основании этих двух неравенств можно записать двойное неравенство

Умножение и деление степеней

Тогда их произведение можно записать как:

5 4 *5 3 = (5*5*5*5)(5*5*5) = 5*5*5*5*5*5*5 = 5 7

Получается, что если перемножаются степени с одинаковым основанием, то в результате получается ещё одна степень с таким же основанием, чей показатель равен сумме показателей перемножаемых степеней. В виде формулы это записывается так:

Это правило умножения степеней называют основным свойством степени. Доказывается оно так:

Аналогично можно перемножить и более двух чисел. Например,

3 2 *3 3 *3 4 = 3 2+3+4 = 3 9

Теперь попробуем понять, как делить степени с одинаковыми основаниями.

Для этого запишем произведение чисел a m – n и a n :

a m – n * a n = a m – n+n = a m+(n-n) = a m+0 = a m

2 10-6 *2 6 = 2 10-6+6 = 2 10

Поделим правую и левую часть этого равенства на 2 6 :

Получается, что верно следующее правило деления степеней:

Данные правила действуют и в том случае, когда вместо показателя и/или основания используется переменная. Например:

Если в выражении есть и умножение, и деление, то следует сначала сложить показатели перемножаемых чисел, а потом вычесть из нее показатели делителей:

Теперь введем понятие нулевой степени числа. Для этого поделим a n на само себя, учитывая уже сформулированные правила деления:

a n : a n = a n-n = a 0

С другой стороны, любое число (кроме нуля), при делении на само себя дает единицу:

Из этих двух равенств можно составить третье равенство:

Получается, что любое число в нулевой степени равно единице.

К выражению 0 0 подобная логика неприменима, так как деление на ноль не допускается в алгебре. Поэтому считается, что выражение 0 0 не имеет смысла, так же как и деление на ноль.

Иногда приходится возводить в степень другую степень. Попытаемся вычислить выражение (2 3 ) 4 :

(2 3 ) 4 = 2 3 * 2 3 * 2 3 * 2 3 = 2 3+3+3+3 = 2 3*4 = 2 12

Видно, что нам пришлось перемножить показатели. Верно следующее правило возведения степени в степень:

Решение. У делимого и делителя разные основания, поэтому сразу произвести деление не получится. Однако число 9 можно представить как квадрат тройки:

Тогда и выражение можно переписать:

9 10 : 3 18 = (3 2 ) 10 : 3 18

Далее последовательно выполняем математические операции:

(3 2 ) 10 : 3 18 = 3 2* 10 : 3 18 = 3 2 0 : 3 18 = 3 20-18 = 3 2 = 9

Иногда приходится выполнять операции над степенями с разными основаниями, но одинаковыми показателями. Перемножим числа 2 4 и 3 4 :

Поменяем местами множители:

Аналогичным образом для любых a и b, а также для любого натурального n справедливым будет равенство:

Такие же рассуждения помогают найти формулу и для деления чисел с одинаковыми показателями:

Далее решим несколько примеров:

Решение: 5 6 •2 6 = (5*2) 6 = 10 6 = 1 000 000

а потому можно провести замену:

Одночлен. Умножение одночленов

Также может использоваться термин «моном», который является синонимом одночлена.

Приведем примеры мономов:

Между переменными можно было бы поставить знак умножения, но почти всегда его опускают. Отдельно отметим, что мономом также считается выражение, в котором отсутствует числовой множитель, присутствует только одна переменная или вовсе нет переменных:

То есть обычное число также считается мономом. Смысл в том, что для вычисления значения монома достаточно использовать операцию умножения.

Так как множители в произведении можно переставлять местами, то выражения 4•abc и a•4•bc идентичны друг другу. Для удобства принято записывать их в так называемом стандартном виде одночлена, когда числовой множитель располагается на первом месте. Сам этот множитель называют коэффициентом одночлена:

Коэффициент есть у всех мономов. Если он не указан, то считают, что перед переменными стоит единица:

Соответственно, в таком случае коэффициентом является единица. Если же перед мономом стоит только знак минус, то его коэффициентом является –1:

Следующее важное понятие – степень одночлена. Она равна сумме степеней, стоящих у переменных в мономе. Найдем степени у некоторых одночленов:

Если у переменной в мономе нет степени, то на самом деле она равна единице, так как любое число в 1-ой степени равно самому себе:

Если моном представляет собой отдельное число, то есть не содержит переменных, то его степень равна нулю.

5a 3 b 4 *6a 5 b 7 = 5*a 3 *b 4 *6*a 5 *b 7 = 5*6*a 3 *a 5 *b 4 *b 7

Продолжим вычисление, учитывая правила умножения чисел с одинаковыми основаниями:

5*6*a 3 *a 5 *b 4 *b 7 = (5*6)*(a 3 *a 5 )*(b 4 *b 7 ) = 30*a 3+5 *b 4+7 = 30a 8 b 11

Получается, что мы просто перемножили коэффициенты мономов, а у одинаковых переменных сложили степени.

Здесь важно не перепутать такие две операции, как нахождение степени монома и умножение одночленов. В первом случае мы складываем степени, стоящие у разных переменных в одном мономе. Во втором случае мы складываем степени, стоящие у одинаковых переменных, но в разных (перемножаемых) мономах.

Рассмотрим несколько примеров.

Степень получившегося монома равна 5 + 5 = 10

Решение. В данном случае приведение к стандартному виду значит тоже самое, что и перемножение одночленов:

Возведение одночлена в степень

Периодически в ходе вычислений возникает необходимость возведения одночлена в степень. Посмотрим, как выполняется подобная операция. Пусть надо возвести 2a 3 b 2 c в четвертую степень:

Видно, что каждый множитель монома мы по отдельности возвели в 4-ую степень. Можно сформулировать следующее правило:

Рассмотрим ещё несколько примеров:

Тождества

В данном случае переменная a, содержащаяся в равенстве, может принимать любое значение. Подставим значение a, равное 1:

Получили верное равенство. Подставим другое значение переменной, например, а=2, снова получим верное равенство (9=9). Вообще при любом допустимом значении переменной a всегда будет получаться верное равенство. Такое равенство называют тождеством.

Иногда в тождествах вместо знака равенства используют особый значок «≡». Основные тождества алгебры, которые вы уже встречали ранее – это переместительные законы сложения и умножения:

сочетательные законы сложения и умножения:

а также распределительный закон, позволяющий раскрывать скобки:

Иногда в понятие тождества включают также и равенства, вовсе не содержащие никаких переменных, например:

В качестве примера равенства, не являющегося тождеством, можно привести 5d+10 = 50. Оно будет выполняться только при значении переменной, равной 8, а при всех остальных значениях не выполняться.

Если два выражения равны друг другу при любых значениях переменных, то их называют тождественно равными.Тождественным преобразованием называют замену выражения на другое, тождественно ему равное. В качестве примера тождественного преобразования можно привести запись:

Источник